Comment résoudre les problèmes B15 sans produits dérivés. Utiliser la dérivée pour trouver les valeurs les plus grandes et les plus petites d'une fonction continue sur un intervalle

Qu'est-ce qu'un extremum d'une fonction et quelle est la condition nécessaire pour un extremum ?

L'extremum d'une fonction est le maximum et le minimum de la fonction.

Condition préalable Le maximum et le minimum (extremum) d'une fonction sont les suivants : si la fonction f(x) a un extremum au point x = a, alors à ce stade la dérivée est soit nulle, soit infinie, soit n'existe pas.

Cette condition est nécessaire mais pas suffisante. La dérivée au point x = a peut aller vers zéro, l'infini ou ne pas exister sans que la fonction ait un extremum à ce stade.

Quelle est la condition suffisante pour l'extremum d'une fonction (maximum ou minimum) ?

Première condition :

Si, à proximité suffisante du point x = a, la dérivée f?(x) est positive à gauche de a et négative à droite de a, alors au point x = a la fonction f(x) a maximum

Si, à une proximité suffisante du point x = a, la dérivée f?(x) est négative à gauche de a et positive à droite de a, alors au point x = a la fonction f(x) a minimumà condition que la fonction f(x) soit ici continue.

Au lieu de cela, vous pouvez utiliser le deuxième état suffisant extremum de la fonction :

Laissez au point x = a la dérivée première f?(x) disparaître ; si la dérivée seconde f??(a) est négative, alors la fonction f(x) a un maximum au point x = a, si elle est positive, alors elle a un minimum.

Quel est le point critique d’une fonction et comment le trouver ?

Il s'agit de la valeur de l'argument de la fonction à laquelle la fonction a un extremum (c'est-à-dire un maximum ou un minimum). Pour le trouver, vous avez besoin trouver la dérivée fonction f?(x) et, en l'assimilant à zéro, résoudre l'équation f?(x) = 0. Les racines de cette équation, ainsi que les points auxquels la dérivée de cette fonction n'existe pas, sont des points critiques, c'est-à-dire des valeurs de l'argument auxquelles il peut y avoir un extremum. Ils peuvent être facilement identifiés en regardant graphique dérivé: nous nous intéressons aux valeurs de l'argument auxquelles le graphique de la fonction coupe l'axe des abscisses (axe Ox) et à celles auxquelles le graphique subit des discontinuités.

Par exemple, trouvons extremum d'une parabole.

Fonction y(x) = 3x2 + 2x - 50.

Dérivée de la fonction : y?(x) = 6x + 2

Résolvez l’équation : y?(x) = 0

6x + 2 = 0, 6x = -2, x = -2/6 = -1/3

DANS dans ce cas le point critique est x0=-1/3. C'est avec cette valeur d'argument que la fonction a extrême. À lui trouver, remplacez le nombre trouvé dans l'expression de la fonction au lieu de « x » :

y0 = 3*(-1/3)2 + 2*(-1/3) - 50 = 3*1/9 - 2/3 - 50 = 1/3 - 2/3 - 50 = -1/3 - 50 = -50,333.

Comment déterminer le maximum et le minimum d'une fonction, c'est-à-dire ses valeurs les plus grandes et les plus petites ?

Si le signe de la dérivée lors du passage par le point critique x0 passe de « plus » à « moins », alors x0 est point maximum; si le signe de la dérivée passe de moins à plus, alors x0 est point minimum; si le signe ne change pas, alors au point x0 il n'y a ni maximum ni minimum.

Pour l'exemple considéré :

On prend une valeur arbitraire de l'argument à gauche du point critique : x = -1

À x = -1, la valeur de la dérivée sera y?(-1) = 6*(-1) + 2 = -6 + 2 = -4 (c'est-à-dire que le signe est « moins »).

Prenons maintenant une valeur arbitraire de l'argument à droite du point critique : x = 1

À x = 1, la valeur de la dérivée sera y(1) = 6*1 + 2 = 6 + 2 = 8 (c'est-à-dire que le signe est « plus »).

Comme vous pouvez le constater, la dérivée change de signe de moins à plus lorsqu’elle passe par le point critique. Cela signifie qu’à la valeur critique x0 nous avons un point minimum.

Valeur la plus grande et la plus petite d'une fonction sur l'intervalle(sur un segment) sont trouvés en utilisant la même procédure, en tenant uniquement compte du fait que, peut-être, tous les points critiques ne se situeront pas dans l'intervalle spécifié. Les points critiques situés en dehors de l'intervalle doivent être exclus de la considération. S'il n'y a qu'un seul point critique à l'intérieur de l'intervalle, il aura soit un maximum, soit un minimum. Dans ce cas, pour déterminer le plus grand et valeurs les plus basses fonctions, on prend également en compte les valeurs de la fonction aux extrémités de l'intervalle.

Par exemple, trouvons les valeurs les plus grandes et les plus petites de la fonction

y(x) = 3sin(x) - 0,5x

à intervalles :

La dérivée de la fonction est donc

y?(x) = 3cos(x) - 0,5

On résout l'équation 3cos(x) - 0,5 = 0

cos(x) = 0,5/3 = 0,16667

x = ±arccos(0,16667) + 2πk.

On retrouve des points critiques sur l'intervalle [-9; 9] :

x = arccos(0,16667) - 2π*2 = -11,163 (non inclus dans l'intervalle)

x = -arccos(0,16667) – 2π*1 = -7,687

x = arccos(0,16667) - 2π*1 = -4,88

x = -arccos(0,16667) + 2π*0 = -1,403

x = arccos(0,16667) + 2π*0 = 1,403

x = -arccos(0,16667) + 2π*1 = 4,88

x = arccos(0,16667) + 2π*1 = 7,687

x = -arccos(0,16667) + 2π*2 = 11,163 (non inclus dans l'intervalle)

On retrouve les valeurs de la fonction aux valeurs critiques de l'argument :

y(-7,687) = 3cos(-7,687) - 0,5 = 0,885

y(-4,88) = 3cos(-4,88) - 0,5 = 5,398

y(-1,403) = 3cos(-1,403) - 0,5 = -2,256

y(1,403) = 3cos(1,403) - 0,5 = 2,256

y(4,88) = 3cos(4,88) - 0,5 = -5,398

y(7,687) = 3cos(7,687) - 0,5 = -0,885

On voit que sur l'intervalle [-9; 9] valeur la plus élevée la fonction a à x = -4,88 :

x = -4,88, y = 5,398,

et le plus petit - à x = 4,88 :

x = 4,88, y = -5,398.

Sur l'intervalle [-6; -3] nous n'avons qu'un seul point critique : x = -4,88. La valeur de la fonction à x = -4,88 est égale à y = 5,398.

Trouvez la valeur de la fonction aux extrémités de l'intervalle :

y(-6) = 3cos(-6) - 0,5 = 3,838

y(-3) = 3cos(-3) - 0,5 = 1,077

Sur l'intervalle [-6; -3] on a la plus grande valeur de la fonction

y = 5,398 à x = -4,88

la plus petite valeur -

y = 1,077 à x = -3

Comment trouver les points d'inflexion d'un graphe de fonctions et déterminer les côtés convexes et concaves ?

Pour trouver tous les points d'inflexion de la droite y = f(x), vous devez trouver la dérivée seconde, l'assimiler à zéro (résoudre l'équation) et tester toutes les valeurs de x pour lesquelles la dérivée seconde est nulle, infini ou n'existe pas. Si, en passant par l'une de ces valeurs, la dérivée seconde change de signe, alors le graphique de la fonction présente une inflexion en ce point. Si cela ne change pas, alors il n’y a pas de virage.

Les racines de l'équation f? (x) = 0, et aussi points possibles La discontinuité de la fonction et la dérivée seconde divisent le domaine de définition de la fonction en plusieurs intervalles. La convexité sur chacun de leurs intervalles est déterminée par le signe de la dérivée seconde. Si la dérivée seconde en un point de l'intervalle étudié est positive, alors la droite y = f(x) est concave vers le haut, et si elle est négative, alors vers le bas.

Comment trouver les extrema d’une fonction à deux variables ?

Pour trouver les extrema de la fonction f(x,y), différentiable dans le domaine de sa spécification, il faut :

1) trouver les points critiques, et pour cela - résoudre le système d'équations

fh ? (x,y) = 0, pour ? (x,y) = 0

2) pour chaque point critique P0(a;b) rechercher si le signe de la différence reste inchangé

pour tous les points (x;y) suffisamment proches de P0. Si la différence reste positive, alors au point P0 nous avons un minimum, si elle est négative, alors nous avons un maximum. Si la différence ne conserve pas son signe, alors il n’y a pas d’extremum au point P0.

Les extrema de la fonction sont déterminés de la même manière pour plus arguments.

Le processus de recherche des valeurs les plus petites et les plus grandes d'une fonction sur un segment rappelle un vol fascinant autour d'un objet (graphique de fonction) dans un hélicoptère, tirant en certains points avec un canon à longue portée et sélectionnant des points très particuliers. à partir de ces points pour des tirs de contrôle. Les points sont sélectionnés d'une certaine manière et selon certaines règles. Par quelles règles ? Nous en reparlerons plus loin.

Si la fonction oui = f(x) est continue sur l'intervalle [ un, b] , alors il atteint ce segment moins Et valeurs les plus élevées . Cela peut se produire soit dans points extrêmes, ou aux extrémités du segment. Par conséquent, pour trouver moins Et les plus grandes valeurs de la fonction , continu sur l'intervalle [ un, b] , vous devez calculer ses valeurs en tout points critiques et aux extrémités du segment, puis choisissez parmi eux le plus petit et le plus grand.

Supposons, par exemple, que vous souhaitiez déterminer la plus grande valeur de la fonction f(x) sur le segment [ un, b] . Pour ce faire, vous devez trouver tous ses points critiques reposant sur [ un, b] .

Point critique appelé le point auquel fonction définie, et elle dérivé soit égal à zéro, soit n'existe pas. Ensuite, les valeurs de la fonction aux points critiques doivent être calculées. Et enfin, il faut comparer les valeurs de la fonction aux points critiques et aux extrémités du segment ( f(un) Et f(b)). Le plus grand de ces nombres sera la plus grande valeur de la fonction sur le segment [un, b] .

Problèmes de recherche plus petites valeurs de fonction .

Nous recherchons ensemble les valeurs les plus petites et les plus grandes de la fonction

Exemple 1. Trouver les valeurs les plus petites et les plus grandes d'une fonction sur le segment [-1, 2] .

Solution. Trouvez la dérivée de cette fonction. Assumons la dérivée à zéro () et obtenons deux points critiques : et . Pour trouver les plus petites et les plus grandes valeurs d'une fonction sur un segment donné, il suffit de calculer ses valeurs aux extrémités du segment et au point, puisque le point n'appartient pas au segment [-1, 2]. Ces valeurs de fonction sont : , , . Il en résulte que plus petite valeur de fonction(indiqué en rouge sur le graphique ci-dessous), égal à -7, est atteint à l'extrémité droite du segment - au point , et le plus grand(également rouge sur le graphique), est égal à 9, - au point critique.

Si une fonction est continue dans un certain intervalle et que cet intervalle n'est pas un segment (mais est, par exemple, un intervalle ; la différence entre un intervalle et un segment : les points limites de l'intervalle ne sont pas inclus dans l'intervalle, mais les les points limites du segment sont inclus dans le segment), alors parmi les valeurs de la fonction, il ne peut y avoir ni la plus petite ni la plus grande. Ainsi, par exemple, la fonction représentée dans la figure ci-dessous est continue sur ]-∞, +∞[ et n'a pas la plus grande valeur.

Cependant, pour tout intervalle (fermé, ouvert ou infini), la propriété suivante des fonctions continues est vraie.

Exemple 4. Trouver les valeurs les plus petites et les plus grandes d'une fonction sur le segment [-1, 3] .

Solution. On retrouve la dérivée de cette fonction comme la dérivée du quotient :

.

Nous assimilons la dérivée à zéro, ce qui nous donne un point critique : . Il appartient au segment [-1, 3] . Pour trouver les plus petites et les plus grandes valeurs d'une fonction sur un segment donné, on retrouve ses valeurs aux extrémités du segment et au point critique trouvé :

Comparons ces valeurs. Conclusion : égal à -5/13, au point et valeur la plus élevéeégal à 1 au point .

Nous continuons à rechercher ensemble les valeurs les plus petites et les plus grandes de la fonction

Il y a des enseignants qui, au sujet de la recherche des valeurs les plus petites et les plus grandes d'une fonction, ne donnent pas aux élèves des exemples à résoudre plus complexes que ceux qui viennent d'être évoqués, c'est-à-dire ceux dans lesquels la fonction est un polynôme ou un fraction dont le numérateur et le dénominateur sont des polynômes. Mais nous ne nous limiterons pas à de tels exemples, car parmi les enseignants il y a ceux qui aiment forcer les élèves à réfléchir pleinement (la table des dérivées). Par conséquent, le logarithme et la fonction trigonométrique seront utilisés.

Exemple 6. Trouver les valeurs les plus petites et les plus grandes d'une fonction sur le segment .

Solution. On trouve la dérivée de cette fonction comme dérivé du produit :

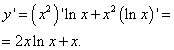
Nous assimilons la dérivée à zéro, ce qui donne un point critique : . Il appartient au segment. Pour trouver les plus petites et les plus grandes valeurs d'une fonction sur un segment donné, on retrouve ses valeurs aux extrémités du segment et au point critique trouvé :

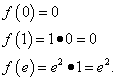
Résultat de toutes les actions : la fonction atteint sa valeur minimale, égal à 0, au point et au point et valeur la plus élevée, égal e², au point.

Exemple 7. Trouver les valeurs les plus petites et les plus grandes d'une fonction sur le segment .

Solution. Trouvez la dérivée de cette fonction :

Nous assimilons la dérivée à zéro :

Le seul point critique appartient au segment. Pour trouver les plus petites et les plus grandes valeurs d'une fonction sur un segment donné, on retrouve ses valeurs aux extrémités du segment et au point critique trouvé :

Conclusion: la fonction atteint sa valeur minimale, égal à , au point et valeur la plus élevée, égal , au point .

Dans les problèmes extrêmes appliqués, trouver les valeurs les plus petites (maximales) d'une fonction revient généralement à trouver le minimum (maximum). Mais ce ne sont pas les minimums ou les maximums eux-mêmes qui présentent le plus grand intérêt pratique, mais les valeurs de l'argumentation auxquelles ils sont atteints. Lors de la résolution de problèmes appliqués, une difficulté supplémentaire surgit : composer des fonctions qui décrivent le phénomène ou le processus considéré.

Exemple 8. Un réservoir d'une capacité de 4, ayant la forme d'un parallélépipède à base carrée et ouvert au sommet, doit être étamé. Quelles doivent être les dimensions du réservoir pour qu'il prenne moindre montant matériel?

Solution. Laisser x- côté socle, h- hauteur du réservoir, S- sa superficie sans couverture, V- son volume. La surface du réservoir est exprimée par la formule, c'est-à-dire est fonction de deux variables. Pour exprimer S en fonction d'une variable, on utilise le fait que , d'où . Remplacement de l'expression trouvée h dans la formule pour S:

Examinons cette fonction à son extremum. Il est défini et différentiable partout dans ]0, +∞[ , et

.

Nous assimilons la dérivée à zéro () et trouvons le point critique. De plus, lorsque la dérivée n'existe pas, mais que cette valeur n'est pas incluse dans le domaine de définition et ne peut donc pas être un point extremum. C’est donc le seul point critique. Vérifions la présence d'un extremum en utilisant le deuxième signe suffisant. Trouvons la dérivée seconde. Lorsque la dérivée seconde est supérieure à zéro (). Cela signifie que lorsque la fonction atteint un minimum . Depuis ce le minimum est le seul extremum de cette fonction, c'est sa plus petite valeur. Ainsi, le côté de la base du réservoir doit être de 2 m et sa hauteur doit être de .

Exemple 9. Du point UN situé sur la voie ferrée, au point AVEC, situé à distance de celui-ci je, la marchandise doit être transportée. Le coût du transport d'une unité de poids par unité de distance par chemin de fer est égal à , et par autoroute, il est égal à . A quel point M. lignes chemin de fer une autoroute devrait être construite pour transporter les marchandises de UN V AVECétait le plus économique (section AB la voie ferrée est supposée être droite) ?

En pratique, il est assez courant d’utiliser la dérivée pour calculer la plus grande et la plus petite valeur d’une fonction. Nous effectuons cette action lorsque nous trouvons comment minimiser les coûts, augmenter les profits, calculer la charge optimale de production, etc., c'est-à-dire dans les cas où nous devons déterminer valeur optimale n’importe quel paramètre. Pour résoudre correctement de tels problèmes, vous devez bien comprendre quelles sont les valeurs les plus grandes et les plus petites d'une fonction.

Yandex.RTB R-A-339285-1

Généralement, nous définissons ces valeurs dans un certain intervalle x, qui à son tour peut correspondre à l'ensemble du domaine de la fonction ou à une partie de celui-ci. Cela peut être comme un segment [a; b ] , et intervalle ouvert (a ; b), (a ; b ], [ a ; b), intervalle infini (a ; b), (a ; b ], [ a ; b) ou intervalle infini - ∞ ; une , (- ∞ ; une ] , [ une ; + ∞) , (- ∞ ; + ∞) .

Dans ce document, nous vous expliquerons comment calculer les valeurs les plus grandes et les plus petites d'une fonction explicitement définie avec une variable y=f(x) y = f (x) .

Définitions de base

Commençons, comme toujours, par la formulation des définitions de base.

Définition 1

La plus grande valeur de la fonction y = f (x) sur un certain intervalle x est la valeur m a x y = f (x 0) x ∈ X, qui pour toute valeur x x ∈ X, x ≠ x 0 fait l'inégalité f (x) ≤ f (x) valide 0) .

Définition 2

La plus petite valeur de la fonction y = f (x) sur un certain intervalle x est la valeur m i n x ∈ X y = f (x 0), ce qui pour toute valeur x ∈ X, x ≠ x 0 fait l'inégalité f(X f (x) ≥ f (x 0) .

Ces définitions sont assez évidentes. Encore plus simple, on peut dire ceci : la plus grande valeur d'une fonction est sa plus grande valeur. grande valeur sur un intervalle connu en abscisse x 0, et la plus petite est la plus petite valeur acceptée sur le même intervalle en x 0.

Définition 3

Les points stationnaires sont les valeurs de l'argument d'une fonction auxquelles sa dérivée devient 0.

Pourquoi avons-nous besoin de savoir ce que sont les points stationnaires ? Pour répondre à cette question, il faut rappeler le théorème de Fermat. Il en résulte qu'un point stationnaire est le point où se situe l'extremum de la fonction différentiable (c'est-à-dire son minimum ou son maximum local). Par conséquent, la fonction prendra la valeur la plus petite ou la plus grande sur un certain intervalle précisément en l'un des points stationnaires.

Une fonction peut également prendre la valeur la plus grande ou la plus petite aux points où la fonction elle-même est définie et où sa dérivée première n'existe pas.

Première question qui se pose lorsqu'on étudie ce sujet : dans tous les cas peut-on déterminer la plus grande ou la plus petite valeur d'une fonction sur un intervalle donné ? Non, nous ne pouvons pas faire cela lorsque les limites d'un intervalle donné coïncident avec les limites de la zone de définition, ou si nous avons affaire à un intervalle infini. Il arrive aussi qu'une fonction dans un segment donné ou à l'infini prenne l'infiniment petit ou l'infini grandes valeurs. Dans ces cas, il n’est pas possible de déterminer la valeur la plus grande et/ou la plus petite.

Ces points deviendront plus clairs après avoir été représentés sur les graphiques :

La première figure nous montre une fonction qui prend les valeurs les plus grandes et les plus petites (m a x y et m i n y) en des points stationnaires situés sur le segment [ - 6 ; 6].

Examinons en détail le cas indiqué dans le deuxième graphique. Changeons la valeur du segment en [ 1 ; 6 ] et nous constatons que la valeur maximale de la fonction sera atteinte au point dont l'abscisse est à la limite droite de l'intervalle, et la valeur minimale au point stationnaire.

Dans la troisième figure, les abscisses des points représentent les points limites du segment [ - 3 ; 2]. Elles correspondent à la plus grande et à la plus petite valeur d'une fonction donnée.

Regardons maintenant la quatrième image. Dans celui-ci, la fonction prend m a x y (la plus grande valeur) et m i n y (la plus petite valeur) à des points stationnaires sur l'intervalle ouvert (- 6 ; 6).

Si l'on prend l'intervalle [ 1 ; 6), alors on peut dire que la plus petite valeur de la fonction sur celui-ci sera atteinte en un point stationnaire. La plus grande valeur nous sera inconnue. La fonction pourrait prendre sa valeur maximale à x égal à 6 si x = 6 appartenait à l'intervalle. C’est exactement le cas montré dans le graphique 5.

Dans le graphique 6, cette fonction acquiert sa plus petite valeur à la limite droite de l'intervalle (- 3 ; 2 ], et nous ne pouvons pas tirer de conclusions définitives sur la plus grande valeur.

Sur la figure 7, nous voyons que la fonction aura m a x y en un point stationnaire ayant une abscisse égale à 1. La fonction atteindra sa valeur minimale à la limite de l'intervalle du côté droit. À moins l'infini, les valeurs de la fonction s'approcheront asymptotiquement de y = 3.

Si l'on prend l'intervalle x ∈ 2 ; + ∞ , alors nous verrons que la fonction donnée ne prendra ni la plus petite ni la plus grande valeur. Si x tend vers 2, alors les valeurs de la fonction tendront vers moins l'infini, puisque la droite x = 2 est une asymptote verticale. Si l'abscisse tend vers plus l'infini, alors les valeurs de la fonction se rapprocheront asymptotiquement de y = 3. C’est exactement le cas illustré à la figure 8.

Dans ce paragraphe, nous présenterons la séquence d'actions à effectuer pour trouver la plus grande ou la plus petite valeur d'une fonction sur un certain segment.

1. Tout d'abord, trouvons le domaine de définition de la fonction. Vérifions si le segment spécifié dans la condition y est inclus.
2. Calculons maintenant les points contenus dans ce segment pour lesquels la dérivée première n'existe pas. Le plus souvent on les retrouve dans des fonctions dont l'argument est écrit sous le signe du module, ou dans fonctions de puissance, dont l’exposant est un nombre fractionnaire rationnel.
3. Ensuite, nous découvrirons quels points stationnaires tomberont dans le segment donné. Pour ce faire, vous devez calculer la dérivée de la fonction, puis l'assimiler à 0 et résoudre l'équation résultante, puis sélectionner les racines appropriées. Si nous n’obtenons pas un seul point stationnaire ou s’il n’appartient pas au segment donné, nous passons à l’étape suivante.
4. Nous déterminons quelles valeurs la fonction prendra à des points stationnaires donnés (le cas échéant), ou à ces points où la dérivée première n'existe pas (s'il y en a), ou nous calculons les valeurs pour x = a et x = b.
5. 5. Nous disposons d’un certain nombre de valeurs de fonction parmi lesquelles nous devons maintenant sélectionner la plus grande et la plus petite. Ce seront les valeurs les plus grandes et les plus petites de la fonction que nous devons trouver.

Voyons comment appliquer correctement cet algorithme lors de la résolution de problèmes.

Exemple 1

Condition: la fonction y = x 3 + 4 x 2 est donnée. Déterminez ses valeurs les plus grandes et les plus petites sur les segments [ 1 ; 4 ] et [ - 4 ; -1 ] .

Solution:

Commençons par trouver le domaine de définition d'une fonction donnée. Dans ce cas, ce sera l’ensemble de tous les nombres réels sauf 0. En d'autres termes, D (y) : x ∈ (- ∞ ; 0) ∪ 0 ; + ∞ . Les deux segments spécifiés dans la condition se trouveront à l'intérieur de la zone de définition.

Calculons maintenant la dérivée de la fonction selon la règle de différenciation des fractions :

y " = x 3 + 4 x 2 " = x 3 + 4 " x 2 - x 3 + 4 x 2 " x 4 = = 3 x 2 x 2 - (x 3 - 4) 2 x x 4 = x 3 - 8 x3

Nous avons appris que la dérivée d'une fonction existera en tout point des segments [ 1 ; 4 ] et [ - 4 ; -1 ] .

Nous devons maintenant déterminer les points stationnaires de la fonction. Faisons cela en utilisant l'équation x 3 - 8 x 3 = 0. Il n’a qu’une seule vraie racine, qui est 2. Ce sera un point stationnaire de la fonction et tombera dans le premier segment [1; 4].

Calculons les valeurs de la fonction aux extrémités du premier segment et à ce stade, c'est-à-dire pour x = 1, x = 2 et x = 4 :

y (1) = 1 3 + 4 1 2 = 5 y (2) = 2 3 + 4 2 2 = 3 y (4) = 4 3 + 4 4 2 = 4 1 4

Nous avons constaté que la plus grande valeur de la fonction m a x y x ∈ [ 1 ; 4 ] = y (2) = 3 sera atteint à x = 1, et le plus petit m i n y x ∈ [ 1 ; 4 ] = y (2) = 3 – à x = 2.

Le deuxième segment ne comprend pas un seul point stationnaire, nous devons donc calculer les valeurs de fonction uniquement aux extrémités du segment donné :

y (- 1) = (- 1) 3 + 4 (- 1) 2 = 3

Cela signifie m a x y x ∈ [ - 4 ; - 1 ] = y (- 1) = 3 , m je n y x ∈ [ - 4 ; - 1 ] = y (- 4) = - 3 3 4 .

Répondre: Pour le segment [ 1 ; 4 ] - m a x y x ∈ [ 1 ; 4 ] = y (2) = 3 , m je n y x ∈ [ 1 ; 4 ] = y (2) = 3 , pour le segment [ - 4 ; - 1 ] - m a x y x ∈ [ - 4 ; - 1 ] = y (- 1) = 3 , m je n y x ∈ [ - 4 ; - 1 ] = y (- 4) = - 3 3 4 .

Voir photo :

Avant d'étudier cette méthode, nous vous conseillons de revoir comment calculer correctement la limite unilatérale et la limite à l'infini, ainsi que d'apprendre les méthodes de base pour les trouver. Pour trouver la plus grande et/ou la plus petite valeur d’une fonction sur un intervalle ouvert ou infini, effectuez les étapes suivantes de manière séquentielle.

1. Vous devez d’abord vérifier si l’intervalle donné est un sous-ensemble du domaine de définition de cette fonction.
2. Déterminons tous les points contenus dans l'intervalle requis et auxquels la dérivée première n'existe pas. Ils se produisent généralement pour les fonctions dont l'argument est entouré du signe du module et pour les fonctions puissance avec un exposant fractionnaire rationnel. Si ces points manquent, vous pouvez alors passer à l'étape suivante.
3. Déterminons maintenant quels points stationnaires se situeront dans l’intervalle donné. Tout d’abord, nous assimilons la dérivée à 0, résolvons l’équation et sélectionnons les racines appropriées. Si nous n'avons pas un seul point stationnaire ou s'ils ne se situent pas dans l'intervalle donné, alors nous passons immédiatement à d'autres actions. Ils sont déterminés par le type d'intervalle.

• Si l'intervalle est de la forme [ a ; b) , alors nous devons calculer la valeur de la fonction au point x = a et la limite unilatérale lim x → b - 0 f (x) .
• Si l'intervalle a la forme (a; b ], alors nous devons calculer la valeur de la fonction au point x = b et la limite unilatérale lim x → a + 0 f (x).
• Si l'intervalle a la forme (a ; b), alors nous devons calculer les limites unilatérales lim x → b - 0 f (x) , lim x → a + 0 f (x) .
• Si l'intervalle est de la forme [ a ; + ∞), alors nous devons calculer la valeur au point x = a et la limite à plus l'infini lim x → + ∞ f (x) .
• Si l'intervalle ressemble à (- ∞ ; b ] , on calcule la valeur au point x = b et la limite à moins l'infini lim x → - ∞ f (x) .
• Si - ∞ ; b , alors nous considérons la limite unilatérale lim x → b - 0 f (x) et la limite à moins l'infini lim x → - ∞ f (x)
• Si - ∞ ; + ∞ , alors on considère les limites sur moins et plus l'infini lim x → + ∞ f (x) , lim x → - ∞ f (x) .

1. À la fin, vous devez tirer une conclusion basée sur les valeurs et limites de la fonction obtenues. De nombreuses options sont disponibles ici. Ainsi, si la limite unilatérale est égale à moins l'infini ou à plus l'infini, alors il est immédiatement clair que rien ne peut être dit sur les valeurs les plus petites et les plus grandes de la fonction. Ci-dessous, nous examinerons un exemple typique. Descriptions détaillées vous aidera à comprendre de quoi il s'agit. Si nécessaire, vous pouvez revenir aux figures 4 à 8 dans la première partie du matériel.

Exemple 2

Condition : fonction donnée y = 3 e 1 x 2 + x - 6 - 4 . Calculez sa plus grande et sa plus petite valeur dans les intervalles - ∞ ; - 4, - ∞ ; - 3 , (- 3 ; 1 ] , (- 3 ; 2) , [ 1 ; 2) , 2 ; + ∞ , [ 4 ; + ∞) .

Solution

Tout d’abord, on retrouve le domaine de définition de la fonction. Le dénominateur de la fraction contient un trinôme quadratique, qui ne doit pas devenir 0 :

x 2 + x - 6 = 0 D = 1 2 - 4 1 (- 6) = 25 x 1 = - 1 - 5 2 = - 3 x 2 = - 1 + 5 2 = 2 ⇒ D (y) : x ∈ (- ∞ ; - 3) ∪ (- 3 ; 2) ∪ (2 ; + ∞)

Nous avons obtenu le domaine de définition de la fonction auquel appartiennent tous les intervalles spécifiés dans la condition.

Maintenant, différencions la fonction et obtenons :

y" = 3 e 1 x 2 + x - 6 - 4 " = 3 e 1 x 2 + x - 6 " = 3 e 1 x 2 + x - 6 1 x 2 + x - 6 " = = 3 · e 1 x 2 + x - 6 · 1" · x 2 + x - 6 - 1 · x 2 + x - 6" (x 2 + x - 6) 2 = - 3 · (2 ​​​​x + 1) · e 1 x 2 + x - 6 x 2 + x - 6 2

Par conséquent, les dérivées d’une fonction existent dans tout son domaine de définition.

Passons à la recherche de points stationnaires. La dérivée de la fonction devient 0 à x = - 1 2 . Il s'agit d'un point stationnaire qui se situe dans les intervalles (- 3 ; 1 ] et (- 3 ; 2) .

Calculons la valeur de la fonction à x = - 4 pour l'intervalle (- ∞ ; - 4 ], ainsi que la limite à moins l'infini :

y (- 4) = 3 e 1 (- 4) 2 + (- 4) - 6 - 4 = 3 e 1 6 - 4 ≈ - 0 . 456 lim x → - ∞ 3 e 1 x 2 + x - 6 = 3 e 0 - 4 = - 1

Puisque 3 e 1 6 - 4 > - 1, cela signifie que m a x y x ∈ (- ∞ ; - 4 ] = y (- 4) = 3 e 1 6 - 4. Cela ne nous permet pas de déterminer de manière unique la plus petite valeur de fonction. On ne peut que conclure qu'il existe une contrainte en dessous de - 1, puisque c'est de cette valeur que la fonction se rapproche asymptotiquement à moins l'infini.

La particularité du deuxième intervalle est qu'il n'y a pas un seul point stationnaire ni une seule limite stricte. Par conséquent, nous ne pourrons calculer ni la plus grande ni la plus petite valeur de la fonction. Après avoir défini la limite à moins l'infini et comme l'argument tend vers - 3 du côté gauche, on obtient seulement un intervalle de valeurs :

lim x → - 3 - 0 3 e 1 x 2 + x - 6 - 4 = lim x → - 3 - 0 3 e 1 (x + 3) (x - 3) - 4 = 3 e 1 (- 3 - 0 + 3) (- 3 - 0 - 2) - 4 = = 3 e 1 (+ 0) - 4 = 3 e + ∞ - 4 = + ∞ lim x → - ∞ 3 e 1 x 2 + x - 6 - 4 = 3 et 0 - 4 = - 1

Cela signifie que les valeurs de la fonction seront situées dans l'intervalle - 1 ; +∞

Pour trouver la plus grande valeur de la fonction dans le troisième intervalle, on détermine sa valeur au point stationnaire x = - 1 2 si x = 1. Nous aurons également besoin de connaître la limite unilatérale pour le cas où l'argument tend vers - 3 du côté droit :

y - 1 2 = 3 e 1 - 1 2 2 + - 1 2 - 6 - 4 = 3 e 4 25 - 4 ≈ - 1 . 444 oui (1) = 3 e 1 1 2 + 1 - 6 - 4 ≈ - 1 . 644 lim x → - 3 + 0 3 e 1 x 2 + x - 6 - 4 = lim x → - 3 + 0 3 e 1 (x + 3) (x - 2) - 4 = 3 e 1 - 3 + 0 + 3 (- 3 + 0 - 2) - 4 = = 3 e 1 (- 0) - 4 = 3 e - ∞ - 4 = 3 0 - 4 = - 4

Il s'est avéré que la fonction prendra la plus grande valeur en un point stationnaire m a x y x ∈ (3; 1 ] = y - 1 2 = 3 e - 4 25 - 4. Quant à la plus petite valeur, nous ne pouvons pas la déterminer. Tout ce que nous savons , est la présence d'une limite inférieure à - 4 .

Pour l'intervalle (- 3 ; 2), prenez les résultats du calcul précédent et calculez à nouveau à quoi est égale la limite unilatérale lorsqu'on tend vers 2 sur le côté gauche :

y - 1 2 = 3 e 1 - 1 2 2 + - 1 2 - 6 - 4 = 3 e - 4 25 - 4 ≈ - 1 . 444 lim x → - 3 + 0 3 e 1 x 2 + x - 6 - 4 = - 4 lim x → 2 - 0 3 e 1 x 2 + x - 6 - 4 = lim x → - 3 + 0 3 e 1 (x + 3) (x - 2) - 4 = 3 e 1 (2 - 0 + 3) (2 - 0 - 2) - 4 = = 3 e 1 - 0 - 4 = 3 e - ∞ - 4 = 3 · 0 - 4 = - 4

Cela signifie que m a x y x ∈ (- 3 ; 2) = y - 1 2 = 3 e - 4 25 - 4, et la plus petite valeur ne peut pas être déterminée, et les valeurs de la fonction sont limitées d'en bas par le nombre - 4 .

D'après ce que nous avons obtenu dans les deux calculs précédents, nous pouvons dire que sur l'intervalle [ 1 ; 2) la fonction prendra la plus grande valeur à x = 1, mais il est impossible de trouver la plus petite.

Sur l'intervalle (2 ; + ∞) la fonction n'atteindra ni la plus grande ni la plus petite valeur, c'est-à-dire il prendra les valeurs de l'intervalle - 1 ; + ∞ .

lim x → 2 + 0 3 e 1 x 2 + x - 6 - 4 = lim x → - 3 + 0 3 e 1 (x + 3) (x - 2) - 4 = 3 e 1 (2 + 0 + 3 ) (2 + 0 - 2) - 4 = = 3 e 1 (+ 0) - 4 = 3 e + ∞ - 4 = + ∞ lim x → + ∞ 3 e 1 x 2 + x - 6 - 4 = 3 e 0 - 4 = - 1

Après avoir calculé à quoi sera égale la valeur de la fonction à x = 4, nous découvrons que m a x y x ∈ [ 4 ; + ∞) = y (4) = 3 e 1 14 - 4 , et la fonction donnée à plus l'infini s'approchera asymptotiquement de la droite y = - 1 .

Comparons ce que nous avons obtenu dans chaque calcul avec le graphique de la fonction donnée. Sur la figure, les asymptotes sont représentées par des lignes pointillées.

C'est tout ce que nous voulions vous dire sur la recherche des valeurs les plus grandes et les plus petites d'une fonction. Les séquences d'actions que nous vous avons données vous aideront à effectuer les calculs nécessaires le plus rapidement et le plus simplement possible. Mais rappelez-vous qu'il est souvent utile de déterminer d'abord à quels intervalles la fonction diminuera et à quels intervalles elle augmentera, après quoi vous pourrez tirer d'autres conclusions. De cette façon, vous pouvez déterminer plus précisément les valeurs les plus grandes et les plus petites de la fonction et justifier les résultats obtenus.

Si vous remarquez une erreur dans le texte, veuillez la surligner et appuyer sur Ctrl+Entrée

Parfois, dans les problèmes B15, il y a des « mauvaises » fonctions pour lesquelles il est difficile de trouver une dérivée. Auparavant, cela ne se produisait que lors de tests par échantillons, mais ces tâches sont désormais si courantes qu'elles ne peuvent plus être ignorées lors de la préparation du véritable examen d'État unifié.

Dans ce cas, d'autres techniques fonctionnent, dont l'une est monotone.

Une fonction f (x) est dite croissante de manière monotone sur le segment si pour l'un des points x 1 et x 2 de ce segment, ce qui suit est vrai :

x1< x 2 ⇒ f (x1) < f (x2).

Une fonction f (x) est dite décroissante de façon monotone sur le segment si pour l'un quelconque des points x 1 et x 2 de ce segment, ce qui suit est vrai :

x1< x 2 ⇒ f (x1) > f ( x2).

En d’autres termes, pour une fonction croissante, plus x est grand, plus f(x) est grand. Pour une fonction décroissante, l’inverse est vrai : plus x est grand, plus moins f(x).

Par exemple, le logarithme augmente de façon monotone si la base a > 1, et diminue de façon monotone si 0< a < 1. Не забывайте про область допустимых значений логарифма: x > 0.

f (x) = log a x (a > 0 ; a ≠ 1 ; x > 0)

La racine carrée arithmétique (et pas seulement carrée) augmente de façon monotone sur tout le domaine de définition :

La fonction exponentielle se comporte de manière similaire au logarithme : elle augmente pour a > 1 et décroît pour 0< a < 1. Но в отличие от логарифма, показательная функция определена для всех чисел, а не только для x > 0:

f (x) = une x (une > 0)

Enfin, les degrés avec un exposant négatif. Vous pouvez les écrire sous forme de fraction. Ils ont un point de rupture où la monotonie est rompue.

Toutes ces fonctions ne se retrouvent jamais dans forme pure. Ils ajoutent des polynômes, des fractions et d'autres absurdités, ce qui rend difficile le calcul de la dérivée. Regardons ce qui se passe dans ce cas.

Coordonnées du sommet de la parabole

Le plus souvent, l'argument de la fonction est remplacé par trinôme quadratique de la forme y = ax 2 + bx + c. Son graphique est une parabole étalon à laquelle on s'intéresse :

1. Les branches d'une parabole peuvent monter (pour a > 0) ou descendre (a< 0). Задают направление, в котором функция может принимать бесконечные значения;
2. Le sommet d'une parabole est le point extremum d'une fonction quadratique auquel cette fonction prend son minimum (pour a > 0) ou son maximum (a< 0) значение.

Le plus grand intérêt est sommet de la parabole, dont l'abscisse est calculée par la formule :

Nous avons donc trouvé le point extrême de la fonction quadratique. Mais si la fonction originale est monotone, pour elle le point x 0 sera aussi un point extremum. Formulons donc la règle clé :

Points extrêmes trinôme quadratique et la fonction complexe dans laquelle il est inclus coïncident. Par conséquent, vous pouvez rechercher x 0 pour un trinôme quadratique et oublier la fonction.

D’après le raisonnement ci-dessus, il reste difficile de savoir quel point nous obtenons : maximum ou minimum. Cependant, les tâches sont spécifiquement conçues pour que cela n'ait pas d'importance. Jugez par vous-même :

1. Il n'y a aucun segment dans l'énoncé du problème. Il n’est donc pas nécessaire de calculer f(a) et f(b). Il ne reste plus qu'à considérer les points extrêmes ;
2. Mais il n'y a qu'un seul point de ce type - c'est le sommet de la parabole x 0, dont les coordonnées sont calculées littéralement oralement et sans aucune dérivée.

Ainsi, la résolution du problème est grandement simplifiée et se résume à seulement deux étapes :

1. Écrivez l'équation de la parabole y = ax 2 + bx + c et trouvez son sommet en utilisant la formule : x 0 = −b /2a ;
2. Trouvez la valeur de la fonction d'origine à ce stade : f (x 0). Si non conditions supplémentaires non, ce sera la réponse.

À première vue, cet algorithme et sa logique peuvent paraître complexes. Je ne publie délibérément pas de diagramme de solution « simple », car l'application irréfléchie de telles règles est semée d'erreurs.

Examinons les vrais problèmes de essai Examen d'État unifié en mathématiques - c'est là que l'on retrouve le plus souvent cette technique. En même temps, nous veillerons à ce que de cette manière de nombreux problèmes liés au B15 deviennent presque oraux.

Sous les racines se dresse fonction quadratique y = x 2 + 6x + 13. Le graphique de cette fonction est une parabole avec des branches vers le haut, puisque le coefficient a = 1 > 0.

Sommet de la parabole :

x 0 = −b /(2a ) = −6/(2 1) = −6/2 = −3

Puisque les branches de la parabole sont dirigées vers le haut, au point x 0 = −3 la fonction y = x 2 + 6x + 13 prend sa valeur minimale.

La racine augmente de manière monotone, ce qui signifie que x 0 est le point minimum de toute la fonction. Nous avons:

Tâche. Trouvez la plus petite valeur de la fonction :

y = log 2 (x 2 + 2x + 9)

Sous le logarithme il y a encore une fonction quadratique : y = x 2 + 2x + 9. Le graphique est une parabole avec des branches vers le haut, car une = 1 > 0.

Sommet de la parabole :

x 0 = −b /(2a ) = −2/(2 1) = −2/2 = −1

Ainsi, au point x 0 = −1 la fonction quadratique prend sa valeur minimale. Mais la fonction y = log 2 x est monotone, donc :

y min = y (−1) = log 2 ((−1) 2 + 2 · (−1) + 9) = ... = log 2 8 = 3

L'exposant contient la fonction quadratique y = 1 − 4x − x 2 . Réécrivons-le sous forme normale : y = −x 2 − 4x + 1.

Évidemment, le graphique de cette fonction est une parabole, avec des branches descendantes (a = −1< 0). Поэтому вершина будет точкой максимума:

x 0 = −b /(2a ) = −(−4)/(2 · (−1)) = 4/(−2) = −2

La fonction d'origine est exponentielle, elle est monotone, donc la plus grande valeur sera au point trouvé x 0 = −2 :

Un lecteur attentif remarquera probablement que nous n'avons pas écrit la plage de valeurs admissibles de la racine et du logarithme. Mais ce n'était pas obligatoire : à l'intérieur se trouvent des fonctions dont les valeurs sont toujours positives.

Corollaires du domaine d'une fonction

Parfois, trouver simplement le sommet de la parabole ne suffit pas à résoudre le problème B15. La valeur que vous recherchez peut mentir à la fin du segment, et pas du tout à l'extrême. Si le problème n'indique aucun segment, regardez plage de valeurs acceptables fonction originale. À savoir:

Attention encore : zéro peut très bien être sous la racine, mais jamais dans le logarithme ou le dénominateur d'une fraction. Voyons comment cela fonctionne avec des exemples spécifiques :

Tâche. Trouvez la plus grande valeur de la fonction :

Sous la racine se trouve à nouveau une fonction quadratique : y = 3 − 2x − x 2 . Son graphique est une parabole, mais ses branches descendent car a = −1< 0. Значит, парабола уходит на минус бесконечность, что недопустимо, поскольку арифметический racine carrée d’un nombre négatif n’existe pas.

Nous écrivons la plage de valeurs admissibles (APV) :

3 − 2x − x 2 ≥ 0 ⇒ x 2 + 2x − 3 ≤ 0 ⇒ (x + 3)(x − 1) ≤ 0 ⇒ x ∈ [−3; 1]

Trouvons maintenant le sommet de la parabole :

x 0 = −b /(2a ) = −(−2)/(2 · (−1)) = 2/(−2) = −1

Le point x 0 = −1 appartient au segment ODZ - et c'est bien. Calculons maintenant la valeur de la fonction au point x 0, ainsi qu'aux extrémités de l'ODZ :

y(−3) = y(1) = 0

Nous avons donc obtenu les nombres 2 et 0. On nous demande de trouver le plus grand - c'est le nombre 2.

Tâche. Trouvez la plus petite valeur de la fonction :

y = log 0,5 (6x − x 2 − 5)

À l'intérieur du logarithme se trouve une fonction quadratique y = 6x − x 2 − 5. C'est une parabole avec des branches vers le bas, mais dans un logarithme il ne peut y avoir nombres négatifs, nous écrivons donc l'ODZ :

6x − x 2 − 5 > 0 ⇒ x 2 − 6x + 5< 0 ⇒ (x − 1)(x − 5) < 0 ⇒ x ∈ (1; 5)

Attention : l'inégalité est stricte, les extrémités n'appartiennent donc pas à l'ODZ. Cela diffère du logarithme de la racine, où les extrémités du segment nous conviennent assez bien.

On cherche le sommet de la parabole :

x 0 = −b /(2a ) = −6/(2 · (−1)) = −6/(−2) = 3

Le sommet de la parabole s'ajuste selon l'ODZ : x 0 = 3 ∈ (1 ; 5). Mais comme on ne s'intéresse pas aux extrémités du segment, on calcule la valeur de la fonction uniquement au point x 0 :

y min = y (3) = log 0,5 (6 3 − 3 2 − 5) = log 0,5 (18 − 9 − 5) = log 0,5 4 = −2

Comment trouver les plus grandes et les plus petites valeurs d'une fonction sur un segment ?

Pour ça nous suivons un algorithme bien connu:

1 . On retrouve les fonctions ODZ.

2 . Trouver la dérivée de la fonction

3 . Égaliser la dérivée à zéro

4 . On trouve les intervalles sur lesquels la dérivée conserve son signe, et à partir d'eux on détermine les intervalles d'augmentation et de diminution de la fonction :

Si sur l'intervalle I la dérivée de la fonction est 0" title="f^(prime)(x)>0">, то функция !} augmente sur cet intervalle.

Si sur l'intervalle I la dérivée de la fonction , alors la fonction diminue sur cet intervalle.

5 . Nous trouvons points maximum et minimum de la fonction.

DANS au point maximum de la fonction, la dérivée change de signe de « + » à « - ».

DANS point minimum de la fonctionla dérivée change de signe de "-" à "+".

6 . On retrouve la valeur de la fonction aux extrémités du segment,

• puis on compare la valeur de la fonction aux extrémités du segment et aux points maximum, et choisissez la plus grande d'entre elles si vous avez besoin de trouver la plus grande valeur de la fonction
• ou comparer la valeur de la fonction aux extrémités du segment et aux points minimaux, et choisissez la plus petite d'entre elles si vous avez besoin de trouver la plus petite valeur de la fonction

Cependant, selon le comportement de la fonction sur le segment, cet algorithme peut être considérablement réduit.

Considérez la fonction . Le graphique de cette fonction ressemble à ceci :

Examinons plusieurs exemples de résolution de problèmes de Banque ouverte tâches pour

1. Tâche B15 (n° 26695)

Sur le segment.

1. La fonction est définie pour toutes les valeurs réelles de x

Évidemment, cette équation n'a pas de solution, et la dérivée est positive pour toutes les valeurs de x. Par conséquent, la fonction augmente et prend la plus grande valeur à l’extrémité droite de l’intervalle, c’est-à-dire en x=0.

Réponse : 5.

2 . Tâche B15 (n° 26702)

Trouver la plus grande valeur de la fonction sur le segment.

1. Fonctions ODZ title="x(pi)/2+(pi)k, k(in)(bbZ)">!}

La dérivée est égale à zéro en , cependant, à ces moments-là, elle ne change pas de signe :

Par conséquent, title="3/(cos^2(x))>=3">, значит, title="3/(cos^2(x))-3>=0">, то есть производная при всех допустимых значених х неотрицательна, следовательно, функция !} augmente et prend la plus grande valeur à l’extrémité droite de l’intervalle, à .

Pour expliquer pourquoi la dérivée ne change pas de signe, nous transformons l'expression de la dérivée comme suit :

Titre="y^(prime)=3/(cos^2(x))-3=(3-3cos^2(x))/(cos^2(x))=(3sin^2 (x))/(cos^2(x))=3tg^2(x)>=0">!}

Réponse : 5.

3. Tâche B15 (n° 26708)

Trouvez la plus petite valeur de la fonction sur le segment.

1. Fonctions ODZ : title="x(pi)/2+(pi)k, k(in)(bbZ)">!}

Plaçons les racines de cette équation sur le cercle trigonométrique.

L'intervalle contient deux nombres : et

Mettons des panneaux. Pour ce faire, on détermine le signe de la dérivée au point x=0 : . En passant par les points et, la dérivée change de signe.

Représentons le changement de signes de la dérivée d'une fonction sur la droite de coordonnées :

Évidemment, le point est un point minimum (auquel la dérivée change de signe de « - » à « + »), et pour trouver la plus petite valeur de la fonction sur le segment, il faut comparer les valeurs de la fonction à le point minimum et à l'extrémité gauche du segment, .