Comment trouver la plus petite valeur d'une fonction. Utiliser la dérivée pour trouver les valeurs les plus grandes et les plus petites d'une fonction continue sur un intervalle

La leçon sur le thème « Utiliser la dérivée pour trouver les valeurs les plus grandes et les plus petites d'une fonction continue sur un intervalle » examinera des problèmes relativement simples de recherche des valeurs les plus grandes et les plus petites d'une fonction sur un intervalle donné à l'aide de la dérivée. .

Sujet : Dérivé

Leçon : Utiliser la dérivée pour trouver les valeurs les plus grandes et les plus petites d'une fonction continue sur un intervalle

Dans cette leçon, nous considérerons un problème plus simple, à savoir, un intervalle sera donné, une fonction continue sera donnée sur cet intervalle. Nous devons connaître la plus grande et la plus petite valeur d'un élément donné. les fonctions sur une donnée entre.

N° 32.1 (b). Donné: , . Traçons un graphique de la fonction (voir Fig. 1).

Riz. 1. Graphique d'une fonction.

On sait que cette fonction augmente sur l'intervalle, ce qui signifie qu'elle augmente également sur l'intervalle. Cela signifie que si vous trouvez la valeur d'une fonction aux points et , alors les limites de changement de cette fonction, ses valeurs les plus grandes et les plus petites seront connues.

Lorsque l’argument passe de à 8, la fonction passe de à .

Répondre: ; .

N° 32.2 (a) Étant donné : Trouver les valeurs les plus grandes et les plus petites de la fonction sur un intervalle donné.

Traçons cette fonction (voir Fig. 2).

Si l'argument change au cours de l'intervalle, alors la fonction passe de -2 à 2. Si l'argument augmente à partir de , alors la fonction diminue de 2 à 0.

Riz. 2. Graphique de fonction.

Trouvons la dérivée.

, . Si , alors cette valeur appartient également au segment donné. Si donc. Il est facile de vérifier s'il prend d'autres valeurs et que les points stationnaires correspondants tombent en dehors du segment donné. Comparons les valeurs de la fonction aux extrémités du segment et aux points sélectionnés auxquels la dérivée est égale à zéro. Nous trouverons

;

Répondre: ;.

La réponse a donc été reçue. Dans ce cas, vous pouvez utiliser la dérivée, vous ne pouvez pas l'utiliser, vous pouvez appliquer les propriétés de la fonction étudiées précédemment. Cela n'arrive pas toujours ; parfois, l'utilisation d'un dérivé est la seule méthode qui permet de résoudre de tels problèmes.

Donné: , . Trouvez les valeurs les plus grandes et les plus petites de la fonction sur un segment donné.

Si dans le cas précédent il était possible de se passer de la dérivée - nous savions comment la fonction se comportait, alors dans ce cas la fonction est assez complexe. Par conséquent, la méthodologie que nous avons mentionnée dans la tâche précédente est pleinement applicable.

1. Trouvons la dérivée. Trouvons les points critiques, donc - les points critiques. Parmi eux, nous sélectionnons ceux qui appartiennent à ce segment : . Comparons la valeur de la fonction aux points , , . Pour cela nous trouverons

Illustrons le résultat sur la figure (voir Fig. 3).

Riz. 3. Limites des modifications des valeurs des fonctions

On voit que si l'argument passe de 0 à 2, la fonction change dans la plage de -3 à 4. La fonction ne change pas de manière monotone : elle augmente ou diminue.

Répondre: ;.

Ainsi, à l'aide de trois exemples, la technique générale permettant de trouver les valeurs les plus grandes et les plus petites d'une fonction sur un intervalle, en l'occurrence sur un segment, a été démontrée.

Algorithme pour résoudre le problème de trouver les valeurs les plus grandes et les plus petites d'une fonction :

1. Trouvez la dérivée de la fonction.

2. Recherchez les points critiques de la fonction et sélectionnez les points qui se trouvent sur un segment donné.

3. Recherchez les valeurs de la fonction aux extrémités du segment et aux points sélectionnés.

4. Comparez ces valeurs et choisissez la plus grande et la plus petite.

Regardons un autre exemple.

Trouvez la plus grande et la plus petite valeur de la fonction , .

Le graphique de cette fonction a été précédemment considéré (voir Fig. 4).

Riz. 4. Graphique de fonction.

Sur l'intervalle, la plage de valeurs de cette fonction . Point - point maximum. Quand - la fonction augmente, quand - la fonction diminue. D'après le dessin, il est clair que , - n'existe pas.

Ainsi, dans la leçon, nous avons examiné le problème des valeurs les plus grandes et les plus petites d'une fonction lorsque l'intervalle donné est un segment ; formulé un algorithme pour résoudre de tels problèmes.

1. Algèbre et début d'analyse, 10e année (en deux parties). Manuel pour les établissements d'enseignement général (niveau profil), éd. A. G. Mordkovitch. -M. : Mnémosyne, 2009.

2. Algèbre et début d'analyse, 10e année (en deux parties). Cahier de problèmes pour les établissements d'enseignement (niveau profil), éd. A. G. Mordkovitch. -M. : Mnémosyne, 2007.

3. Vilenkin N.Ya., Ivashev-Musatov O.S., Shvartsburd S.I. Algèbre et analyse mathématique pour la 10e année (manuel pour les élèves des écoles et classes avec études avancées de mathématiques - M. : Prosveshchenie, 1996).

4. Galitsky M.L., Moshkovich M.M., Shvartsburd S.I. Étude approfondie de l'algèbre et de l'analyse mathématique.-M. : Education, 1997.

5. Recueil de problèmes de mathématiques pour les candidats aux établissements d'enseignement supérieur (édité par M.I. Skanavi - M. : Higher School, 1992).

6. Merzlyak A.G., Polonsky V.B., Yakir M.S. Simulateur algébrique.-K. : A.S.K., 1997.

7. Zvavich L.I., Shlyapochnik L.Ya., Chinkina Algebra et les débuts de l'analyse. 8e-11e années : Un manuel pour les écoles et les classes avec une étude approfondie des mathématiques (matériel didactique - M. : Outarde, 2002).

8. Sahakyan S.M., Goldman A.M., Denisov D.V. Problèmes d'algèbre et principes d'analyse (un manuel pour les étudiants de la 10e à la 11e année des établissements d'enseignement général - M. : Prosveshchenie, 2003).

9. Karp A.P. Recueil de problèmes sur l'algèbre et principes d'analyse : manuel. allocation pour les classes 10-11. avec profondeur étudié Mathématiques.-M. : Éducation, 2006.

10. Glazer G.I. Histoire des mathématiques à l'école. 9e et 10e années (manuel pour les enseignants).-M. : Éducation, 1983

Ressources Web supplémentaires

2. Portail des sciences naturelles ().

Faites-le à la maison

N° 46.16, 46.17 (c) (Algèbre et débuts de l'analyse, 10e année (en deux parties). Livre de problèmes pour les établissements d'enseignement général (niveau profil) édité par A. G. Mordkovich. - M. : Mnemozina, 2007.)

D'un point de vue pratique, le plus grand intérêt est d'utiliser la dérivée pour trouver les plus grandes et les plus petites valeurs d'une fonction. A quoi est-ce lié ? Maximiser les profits, minimiser les coûts, déterminer la charge optimale des équipements... En d'autres termes, dans de nombreux domaines de la vie, nous devons résoudre des problèmes d'optimisation de certains paramètres. Et ce sont les tâches consistant à trouver les valeurs les plus grandes et les plus petites d'une fonction.

Il convient de noter que les valeurs les plus grandes et les plus petites d'une fonction sont généralement recherchées sur un certain intervalle X, qui est soit le domaine entier de la fonction, soit une partie du domaine de définition. L'intervalle X lui-même peut être un segment, un intervalle ouvert , un intervalle infini.

Dans cet article, nous parlerons de la recherche des valeurs les plus grandes et les plus petites d'une fonction explicitement définie d'une variable y=f(x) .

Navigation dans les pages.

La plus grande et la plus petite valeur d'une fonction - définitions, illustrations.

Examinons brièvement les principales définitions.

La plus grande valeur de la fonction ça pour n'importe qui l’inégalité est vraie.

La plus petite valeur de la fonction y=f(x) sur l'intervalle X est appelé une telle valeur ça pour n'importe qui l’inégalité est vraie.

Ces définitions sont intuitives : la plus grande (la plus petite) valeur d'une fonction est la plus grande (la plus petite) valeur acceptée sur l'intervalle considéré en abscisse.

Points fixes– ce sont les valeurs de l'argument pour lesquelles la dérivée de la fonction devient nulle.

Pourquoi avons-nous besoin de points stationnaires pour trouver les valeurs les plus grandes et les plus petites ? La réponse à cette question est donnée par le théorème de Fermat. De ce théorème, il s'ensuit que si une fonction différentiable a un extremum (minimum local ou maximum local) en un certain point, alors ce point est stationnaire. Ainsi, la fonction prend souvent sa plus grande (plus petite) valeur sur l'intervalle X en l'un des points stationnaires de cet intervalle.

De plus, une fonction peut souvent prendre ses valeurs les plus grandes et les plus petites aux points où la dérivée première de cette fonction n'existe pas et la fonction elle-même est définie.

Répondons immédiatement à l’une des questions les plus courantes sur ce sujet : « Est-il toujours possible de déterminer la plus grande (la plus petite) valeur d’une fonction » ? Non, pas toujours. Parfois les limites de l'intervalle X coïncident avec les limites du domaine de définition de la fonction, ou l'intervalle X est infini. Et certaines fonctions à l'infini et aux limites du domaine de définition peuvent prendre à la fois des valeurs infiniment grandes et des valeurs infiniment petites. Dans ces cas, on ne peut rien dire sur la valeur la plus grande et la plus petite de la fonction.

Pour plus de clarté, nous donnerons une illustration graphique. Regardez les images et beaucoup de choses deviendront plus claires.

Sur le segment

Dans la première figure, la fonction prend les valeurs les plus grandes (max y) et les plus petites (min y) aux points stationnaires situés à l'intérieur du segment [-6;6].

Prenons le cas représenté dans la deuxième figure. Changeons le segment en . Dans cet exemple, la plus petite valeur de la fonction est obtenue en un point stationnaire, et la plus grande au point dont l'abscisse correspond à la limite droite de l'intervalle.

Sur la figure 3, les points limites du segment [-3;2] sont les abscisses des points correspondant à la plus grande et à la plus petite valeur de la fonction.

Sur un intervalle ouvert

Dans la quatrième figure, la fonction prend les valeurs les plus grandes (max y) et les plus petites (min y) aux points stationnaires situés à l'intérieur de l'intervalle ouvert (-6;6).

Sur l'intervalle, aucune conclusion ne peut être tirée sur la plus grande valeur.

À l'infini

Dans l'exemple présenté sur la septième figure, la fonction prend la plus grande valeur (max y) en un point stationnaire d'abscisse x=1, et la plus petite valeur (min y) est obtenue sur la limite droite de l'intervalle. À moins l'infini, les valeurs de la fonction se rapprochent asymptotiquement de y=3.

Sur l'intervalle, la fonction n'atteint ni la plus petite ni la plus grande valeur. À mesure que x=2 s'approche de la droite, les valeurs de la fonction tendent vers moins l'infini (la droite x=2 est une asymptote verticale), et lorsque l'abscisse tend vers plus l'infini, les valeurs de la fonction se rapprochent asymptotiquement de y=3. Une illustration graphique de cet exemple est présentée à la figure 8.

Algorithme pour trouver les valeurs les plus grandes et les plus petites d'une fonction continue sur un segment.

Écrivons un algorithme qui nous permet de trouver les valeurs les plus grandes et les plus petites d'une fonction sur un segment.

1. On retrouve le domaine de définition de la fonction et on vérifie si elle contient le segment entier.
2. Nous trouvons tous les points auxquels la dérivée première n'existe pas et qui sont contenus dans le segment (généralement, ces points se trouvent dans les fonctions avec un argument sous le signe du module et dans les fonctions puissance avec un exposant fractionnaire-rationnel). S'il n'y a pas de tels points, passez au point suivant.
3. Nous déterminons tous les points stationnaires tombant dans le segment. Pour ce faire, nous l'assimilons à zéro, résolvons l'équation résultante et sélectionnons les racines appropriées. S'il n'y a pas de points fixes ou si aucun d'entre eux ne tombe dans le segment, passez au point suivant.
4. Nous calculons les valeurs de la fonction en des points stationnaires sélectionnés (le cas échéant), en des points où la dérivée première n'existe pas (le cas échéant), ainsi qu'en x=a et x=b.
5. À partir des valeurs obtenues de la fonction, nous sélectionnons la plus grande et la plus petite - ce seront respectivement les valeurs les plus grandes et les plus petites requises de la fonction.

Analysons l'algorithme de résolution d'un exemple pour trouver les valeurs les plus grandes et les plus petites d'une fonction sur un segment.

Exemple.

Trouver la plus grande et la plus petite valeur d'une fonction

• sur le segment ;
• sur le segment [-4;-1] .

Solution.

Le domaine de définition d’une fonction est l’ensemble des nombres réels, à l’exception de zéro. Les deux segments relèvent du domaine de définition.

Trouver la dérivée de la fonction par rapport à :

Évidemment, la dérivée de la fonction existe en tout point des segments et [-4;-1].

Nous déterminons les points stationnaires à partir de l'équation. La seule vraie racine est x=2. Ce point stationnaire appartient au premier segment.

Pour le premier cas, on calcule les valeurs de la fonction aux extrémités du segment et au point stationnaire, c'est-à-dire pour x=1, x=2 et x=4 :

Donc la plus grande valeur de la fonction est atteint à x=1, et la plus petite valeur – à x=2.

Pour le deuxième cas, on calcule les valeurs de la fonction uniquement aux extrémités du segment [-4;-1] (puisqu'il ne contient pas un seul point stationnaire) :

Le processus de recherche des valeurs les plus petites et les plus grandes d'une fonction sur un segment rappelle un vol fascinant autour d'un objet (graphique d'une fonction) dans un hélicoptère, tirant en certains points avec un canon à longue portée et sélectionnant très points spéciaux à partir de ces points pour les tirs de contrôle. Les points sont sélectionnés d'une certaine manière et selon certaines règles. Par quelles règles ? Nous en reparlerons plus loin.

Si la fonction oui = F(X) est continue sur l'intervalle [ un, b] , alors il atteint ce segment moins Et valeurs les plus élevées . Cela peut se produire soit dans points extrêmes, ou aux extrémités du segment. Par conséquent, pour trouver moins Et les plus grandes valeurs de la fonction , continu sur l'intervalle [ un, b] , vous devez calculer ses valeurs en tout points critiques et aux extrémités du segment, puis choisissez parmi eux le plus petit et le plus grand.

Supposons, par exemple, que vous souhaitiez déterminer la plus grande valeur de la fonction F(X) sur le segment [ un, b] . Pour ce faire, vous devez trouver tous ses points critiques reposant sur [ un, b] .

Point critique appelé le point auquel fonction définie, et elle dérivé soit égal à zéro, soit n'existe pas. Ensuite, vous devez calculer les valeurs de la fonction aux points critiques. Et enfin, il faut comparer les valeurs de la fonction aux points critiques et aux extrémités du segment ( F(un) Et F(b)). Le plus grand de ces nombres sera la plus grande valeur de la fonction sur le segment [un, b] .

Problèmes de recherche plus petites valeurs de fonction .

Nous recherchons ensemble les valeurs les plus petites et les plus grandes de la fonction

Exemple 1. Trouver les valeurs les plus petites et les plus grandes d'une fonction sur le segment [-1, 2] .

Solution. Trouvez la dérivée de cette fonction. Assumons la dérivée à zéro () et obtenons deux points critiques : et . Pour trouver les plus petites et les plus grandes valeurs d'une fonction sur un segment donné, il suffit de calculer ses valeurs aux extrémités du segment et au point, puisque le point n'appartient pas au segment [-1, 2]. Ces valeurs de fonction sont : , , . Il s'ensuit que plus petite valeur de fonction(indiqué en rouge sur le graphique ci-dessous), égal à -7, est atteint à l'extrémité droite du segment - au point , et le plus grand(également rouge sur le graphique), est égal à 9, - au point critique.

Si une fonction est continue dans un certain intervalle et que cet intervalle n'est pas un segment (mais est, par exemple, un intervalle ; la différence entre un intervalle et un segment : les points limites de l'intervalle ne sont pas inclus dans l'intervalle, mais les les points limites du segment sont inclus dans le segment), alors parmi les valeurs de la fonction, il ne peut y avoir ni la plus petite ni la plus grande. Ainsi, par exemple, la fonction représentée dans la figure ci-dessous est continue sur ]-∞, +∞[ et n'a pas la plus grande valeur.

Cependant, pour tout intervalle (fermé, ouvert ou infini), la propriété suivante des fonctions continues est vraie.

Exemple 4. Trouver les valeurs les plus petites et les plus grandes d'une fonction sur le segment [-1, 3] .

Solution. On retrouve la dérivée de cette fonction comme la dérivée du quotient :

.

Nous assimilons la dérivée à zéro, ce qui nous donne un point critique : . Il appartient au segment [-1, 3]. Pour trouver les plus petites et les plus grandes valeurs d'une fonction sur un segment donné, on retrouve ses valeurs aux extrémités du segment et au point critique trouvé :

Comparons ces valeurs. Conclusion : égal à -5/13, au point et valeur la plus élevéeégal à 1 au point .

Nous continuons à rechercher ensemble les valeurs les plus petites et les plus grandes de la fonction

Il y a des enseignants qui, au sujet de la recherche des valeurs les plus petites et les plus grandes d'une fonction, ne donnent pas aux élèves des exemples à résoudre plus complexes que ceux qui viennent d'être évoqués, c'est-à-dire ceux dans lesquels la fonction est un polynôme ou un fraction dont le numérateur et le dénominateur sont des polynômes. Mais nous ne nous limiterons pas à de tels exemples, car parmi les enseignants il y a ceux qui aiment forcer les élèves à réfléchir pleinement (la table des dérivées). Par conséquent, le logarithme et la fonction trigonométrique seront utilisés.

Exemple 6. Trouver les valeurs les plus petites et les plus grandes d'une fonction sur le segment .

Solution. On trouve la dérivée de cette fonction comme dérivé du produit :

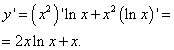
Nous assimilons la dérivée à zéro, ce qui donne un point critique : . Il appartient au segment. Pour trouver les plus petites et les plus grandes valeurs d'une fonction sur un segment donné, on retrouve ses valeurs aux extrémités du segment et au point critique trouvé :

Résultat de toutes les actions : la fonction atteint sa valeur minimale, égal à 0, au point et au point et valeur la plus élevée, égal e², au point.

Exemple 7. Trouver les valeurs les plus petites et les plus grandes d'une fonction sur le segment .

Solution. Trouvez la dérivée de cette fonction :

Nous assimilons la dérivée à zéro :

Le seul point critique appartient au segment. Pour trouver les plus petites et les plus grandes valeurs d'une fonction sur un segment donné, on retrouve ses valeurs aux extrémités du segment et au point critique trouvé :

Conclusion: la fonction atteint sa valeur minimale, égal à , au point et valeur la plus élevée, égal , au point .

Dans les problèmes extrêmes appliqués, trouver les valeurs les plus petites (maximales) d'une fonction revient généralement à trouver le minimum (maximum). Mais ce ne sont pas les minimums ou les maximums eux-mêmes qui présentent le plus grand intérêt pratique, mais les valeurs de l'argumentation auxquelles ils sont atteints. Lors de la résolution de problèmes appliqués, une difficulté supplémentaire surgit : composer des fonctions qui décrivent le phénomène ou le processus considéré.

Exemple 8. Un réservoir d'une capacité de 4, ayant la forme d'un parallélépipède à base carrée et ouvert en haut, doit être étamé. Quelle doit être la taille du réservoir pour que le moins de matériau soit utilisé pour le recouvrir ?

Solution. Laisser X- côté socle, h- hauteur du réservoir, S- sa superficie sans couverture, V- son volume. La surface du réservoir est exprimée par la formule, c'est-à-dire est fonction de deux variables. Exprimer S en fonction d'une variable, on utilise le fait que , d'où . Remplacement de l'expression trouvée h dans la formule pour S:

Examinons cette fonction à son extremum. Il est défini et différentiable partout dans ]0, +∞[ , et

.

Nous assimilons la dérivée à zéro () et trouvons le point critique. De plus, lorsque la dérivée n'existe pas, mais cette valeur n'est pas incluse dans le domaine de définition et ne peut donc pas être un point extremum. C’est donc le seul point critique. Vérifions la présence d'un extremum en utilisant le deuxième signe suffisant. Trouvons la dérivée seconde. Lorsque la dérivée seconde est supérieure à zéro (). Cela signifie que lorsque la fonction atteint un minimum . Depuis cela le minimum est le seul extremum de cette fonction, c'est sa plus petite valeur. Ainsi, le côté de la base du réservoir doit être de 2 m et sa hauteur doit être de .

Exemple 9. Du point UN situé sur la voie ferrée, au point AVEC, situé à distance de celui-ci je, la marchandise doit être transportée. Le coût du transport d'une unité de poids par unité de distance par chemin de fer est égal à , et par autoroute, il est égal à . A quel point M la ligne de chemin de fer devrait être construite comme une autoroute afin que les marchandises puissent être transportées depuis UN V AVECétait le plus économique (section UN B la voie ferrée est supposée être droite) ?

Qu'est-ce qu'un extremum d'une fonction et quelle est la condition nécessaire pour un extremum ?

L'extremum d'une fonction est le maximum et le minimum de la fonction.

La condition nécessaire pour le maximum et le minimum (extremum) d'une fonction est la suivante : si la fonction f(x) a un extremum au point x = a, alors à ce stade la dérivée est soit nulle, soit infinie, ou bien n'existe pas.

Cette condition est nécessaire mais pas suffisante. La dérivée au point x = a peut aller vers zéro, l'infini ou ne pas exister sans que la fonction ait un extremum à ce stade.

Quelle est la condition suffisante pour l'extremum d'une fonction (maximum ou minimum) ?

Première condition :

Si, à proximité suffisante du point x = a, la dérivée f?(x) est positive à gauche de a et négative à droite de a, alors au point x = a la fonction f(x) a maximum

Si, à proximité suffisante du point x = a, la dérivée f?(x) est négative à gauche de a et positive à droite de a, alors au point x = a la fonction f(x) a le minimumà condition que la fonction f(x) soit ici continue.

Au lieu de cela, vous pouvez utiliser la deuxième condition suffisante pour l’extremum d’une fonction :

Laissez au point x = a la dérivée première f?(x) disparaître ; si la dérivée seconde f??(a) est négative, alors la fonction f(x) a un maximum au point x = a, si elle est positive, alors elle a un minimum.

Quel est le point critique d’une fonction et comment le trouver ?

Il s'agit de la valeur de l'argument de la fonction à laquelle la fonction a un extremum (c'est-à-dire un maximum ou un minimum). Pour le trouver, vous avez besoin trouver la dérivée fonction f?(x) et, en l'assimilant à zéro, résous l'équation f?(x) = 0. Les racines de cette équation, ainsi que les points auxquels la dérivée de cette fonction n'existe pas, sont des points critiques, c'est-à-dire des valeurs de l'argument auxquelles il peut y avoir un extremum. Ils peuvent être facilement identifiés en regardant graphique dérivé: nous nous intéressons aux valeurs de l'argument auxquelles le graphique de la fonction coupe l'axe des abscisses (axe Ox) et à celles auxquelles le graphique subit des discontinuités.

Par exemple, trouvons extremum d'une parabole.

Fonction y(x) = 3x2 + 2x - 50.

Dérivée de la fonction : y?(x) = 6x + 2

Résolvez l'équation : y?(x) = 0

6x + 2 = 0, 6x = -2, x = -2/6 = -1/3

Dans ce cas, le point critique est x0=-1/3. C'est avec cette valeur d'argument que la fonction a extrême. À lui trouver, remplacez le nombre trouvé dans l'expression de la fonction au lieu de « x » :

y0 = 3*(-1/3)2 + 2*(-1/3) - 50 = 3*1/9 - 2/3 - 50 = 1/3 - 2/3 - 50 = -1/3 - 50 = -50,333.

Comment déterminer le maximum et le minimum d'une fonction, c'est-à-dire ses valeurs les plus grandes et les plus petites ?

Si le signe de la dérivée lors du passage par le point critique x0 passe de « plus » à « moins », alors x0 est point maximum; si le signe de la dérivée passe de moins à plus, alors x0 est point minimum; si le signe ne change pas, alors au point x0 il n'y a ni maximum ni minimum.

Pour l'exemple considéré :

On prend une valeur arbitraire de l'argument à gauche du point critique : x = -1

À x = -1, la valeur de la dérivée sera y?(-1) = 6*(-1) + 2 = -6 + 2 = -4 (c'est-à-dire que le signe est « moins »).

Prenons maintenant une valeur arbitraire de l'argument à droite du point critique : x = 1

À x = 1, la valeur de la dérivée sera y(1) = 6*1 + 2 = 6 + 2 = 8 (c'est-à-dire que le signe est « plus »).

Comme vous pouvez le constater, la dérivée change de signe de moins à plus lorsqu’elle passe par le point critique. Cela signifie qu’à la valeur critique x0 nous avons un point minimum.

Valeur la plus grande et la plus petite d'une fonction sur l'intervalle(sur un segment) sont trouvés en utilisant la même procédure, en tenant uniquement compte du fait que, peut-être, tous les points critiques ne se situeront pas dans l'intervalle spécifié. Les points critiques situés en dehors de l'intervalle doivent être exclus de la considération. S'il n'y a qu'un seul point critique dans l'intervalle, il aura soit un maximum, soit un minimum. Dans ce cas, pour déterminer les valeurs les plus grandes et les plus petites de la fonction, on prend également en compte les valeurs de la fonction aux extrémités de l'intervalle.

Par exemple, trouvons les valeurs les plus grandes et les plus petites de la fonction

y(x) = 3sin(x) - 0,5x

à intervalles:

La dérivée de la fonction est donc

y?(x) = 3cos(x) - 0,5

On résout l'équation 3cos(x) - 0,5 = 0

cos(x) = 0,5/3 = 0,16667

x = ±arccos(0,16667) + 2πk.

On retrouve des points critiques sur l'intervalle [-9; 9] :

x = arccos(0,16667) - 2π*2 = -11,163 (non inclus dans l'intervalle)

x = -arccos(0,16667) – 2π*1 = -7,687

x = arccos(0,16667) - 2π*1 = -4,88

x = -arccos(0,16667) + 2π*0 = -1,403

x = arccos(0,16667) + 2π*0 = 1,403

x = -arccos(0,16667) + 2π*1 = 4,88

x = arccos(0,16667) + 2π*1 = 7,687

x = -arccos(0,16667) + 2π*2 = 11,163 (non inclus dans l'intervalle)

On retrouve les valeurs de la fonction aux valeurs critiques de l'argument :

y(-7,687) = 3cos(-7,687) - 0,5 = 0,885

y(-4,88) = 3cos(-4,88) - 0,5 = 5,398

y(-1,403) = 3cos(-1,403) - 0,5 = -2,256

y(1,403) = 3cos(1,403) - 0,5 = 2,256

y(4,88) = 3cos(4,88) - 0,5 = -5,398

y(7,687) = 3cos(7,687) - 0,5 = -0,885

On voit que sur l'intervalle [-9; 9] la fonction a la plus grande valeur à x = -4,88 :

x = -4,88, y = 5,398,

et le plus petit - à x = 4,88 :

x = 4,88, y = -5,398.

Sur l'intervalle [-6; -3] nous n'avons qu'un seul point critique : x = -4,88. La valeur de la fonction à x = -4,88 est égale à y = 5,398.

Trouvez la valeur de la fonction aux extrémités de l'intervalle :

y(-6) = 3cos(-6) - 0,5 = 3,838

y(-3) = 3cos(-3) - 0,5 = 1,077

Sur l'intervalle [-6; -3] on a la plus grande valeur de la fonction

y = 5,398 à x = -4,88

la plus petite valeur -

y = 1,077 à x = -3

Comment trouver les points d'inflexion d'un graphe de fonctions et déterminer les côtés convexes et concaves ?

Pour trouver tous les points d'inflexion de la droite y = f(x), vous devez trouver la dérivée seconde, l'assimiler à zéro (résoudre l'équation) et tester toutes les valeurs de x pour lesquelles la dérivée seconde est nulle, infini ou n'existe pas. Si, en passant par l'une de ces valeurs, la dérivée seconde change de signe, alors le graphique de la fonction présente une inflexion en ce point. Si cela ne change pas, alors il n’y a pas de virage.

Les racines de l'équation f? (x) = 0, ainsi que les éventuels points de discontinuité de la fonction et de la dérivée seconde, divisent le domaine de définition de la fonction en un certain nombre d'intervalles. La convexité sur chacun de leurs intervalles est déterminée par le signe de la dérivée seconde. Si la dérivée seconde en un point de l'intervalle étudié est positive, alors la droite y = f(x) est concave vers le haut, et si elle est négative, alors vers le bas.

Comment trouver les extrema d’une fonction à deux variables ?

Pour trouver les extrema de la fonction f(x,y), différentiable dans le domaine de sa spécification, il faut :

1) trouver les points critiques, et pour cela - résoudre le système d'équations

putain ? (x,y) = 0, pour ? (x,y) = 0

2) pour chaque point critique P0(a;b) rechercher si le signe de la différence reste inchangé

pour tous les points (x;y) suffisamment proches de P0. Si la différence reste positive, alors au point P0 nous avons un minimum, si elle est négative, alors nous avons un maximum. Si la différence ne conserve pas son signe, alors il n’y a pas d’extremum au point P0.

Les extrema d’une fonction sont déterminés de la même manière pour un plus grand nombre d’arguments.

Laissez la fonction y =F(X) est continue sur l'intervalle [ un B]. Comme on le sait, une telle fonction atteint ses valeurs maximales et minimales sur ce segment. La fonction peut prendre ces valeurs soit au point interne du segment [ un B], ou sur la limite du segment.

Pour trouver les plus grandes et les plus petites valeurs d'une fonction sur le segment [ un B] nécessaire:

1) trouver les points critiques de la fonction dans l'intervalle ( un B);

2) calculer les valeurs de la fonction aux points critiques trouvés ;

3) calculer les valeurs de la fonction aux extrémités du segment, c'est-à-dire lorsque X=UN et x = b;

4) parmi toutes les valeurs calculées de la fonction, sélectionnez la plus grande et la plus petite.

Exemple. Trouver les valeurs les plus grandes et les plus petites d'une fonction

sur le segment.

Trouver les points critiques :

Ces points se situent à l'intérieur du segment ; oui(1) = ‒ 3; oui(2) = ‒ 4; oui(0) = ‒ 8; oui(3) = 1;

à ce point X= 3 et au point X= 0.

Etude d'une fonction de convexité et de point d'inflexion.

Fonction oui = F (X) appelé convexe entre (un, b) , si son graphique se situe sous la tangente tracée en tout point de cet intervalle, et s'appelle convexe vers le bas (concave), si son graphique se situe au-dessus de la tangente.

Le point par lequel la convexité est remplacée par la concavité ou vice versa est appelé point d'inflexion.

Algorithme d'examen de la convexité et du point d'inflexion :

1. Trouvez les points critiques du deuxième type, c'est-à-dire les points auxquels la dérivée seconde est égale à zéro ou n'existe pas.

2. Tracez les points critiques sur la droite numérique, en la divisant en intervalles. Trouvez le signe de la dérivée seconde sur chaque intervalle ; si , alors la fonction est convexe vers le haut, si, alors la fonction est convexe vers le bas.

3. Si, en passant par un point critique de seconde espèce, le signe change et qu'à ce point la dérivée seconde est égale à zéro, alors ce point est l'abscisse du point d'inflexion. Trouvez son ordonnée.

Asymptotes du graphique d'une fonction. Etude d'une fonction pour les asymptotes.

Définition. L'asymptote du graphe d'une fonction s'appelle droit, qui a la propriété que la distance entre n'importe quel point du graphique et cette ligne tend vers zéro lorsque le point du graphique s'éloigne indéfiniment de l'origine.

Il existe trois types d'asymptotes : vertical, horizontal et incliné.

Définition. La ligne droite s'appelle asymptote verticale graphiques de fonctions y = f(x), si au moins une des limites unilatérales de la fonction en ce point est égale à l'infini, c'est-à-dire

où est le point de discontinuité de la fonction, c'est-à-dire qu'elle n'appartient pas au domaine de définition.

Exemple.

D ( oui) = (‒ ∞; 2) (2; + ∞)

X= 2 – point de rupture.

Définition. Droit y =UN appelé asymptote horizontale graphiques de fonctions y = f(x)à , si

Exemple.

X
oui

Définition. Droit y =kx +b (k≠ 0) est appelé asymptote oblique graphiques de fonctions y = f(x)à , où

Schéma général d'étude des fonctions et de construction de graphiques.

Algorithme de recherche fonctionnelley = f(x) :

1. Trouvez le domaine de la fonction D (oui).

2. Trouver (si possible) les points d'intersection du graphique avec les axes de coordonnées (si X= 0 et à oui = 0).

3. Examinez la régularité et l'impair de la fonction ( oui (‒ X) = oui (X) ‒ parité; oui(‒ X) = ‒ oui (X) ‒ impair).

4. Trouvez les asymptotes du graphique de la fonction.

5. Trouvez les intervalles de monotonie de la fonction.

6. Trouvez les extrema de la fonction.

7. Trouvez les intervalles de convexité (concavité) et les points d'inflexion du graphique de fonctions.

8. Sur la base des recherches effectuées, construisez un graphique de la fonction.

Exemple. Explorez la fonction et construisez son graphique.

1) D (oui) =

X= 4 – point de rupture.

2) Quand X = 0,

(0; ‒ 5) – point d'intersection avec Oh.

À oui = 0,

3) oui(‒ X)= une fonction de forme générale (ni paire ni impaire).

4) Nous recherchons les asymptotes.

a) verticale

b) horizontale

c) trouver les asymptotes obliques où

‒équation asymptote oblique

5) Dans cette équation il n'est pas nécessaire de trouver des intervalles de monotonie de la fonction.

6)

Ces points critiques divisent tout le domaine de définition de la fonction en l'intervalle (˗∞; ˗2), (˗2; 4), (4; 10) et (10; +∞). Il convient de présenter les résultats obtenus sous la forme du tableau suivant.