ศักยภาพในการสร้างสรรค์มักเป็นผลมาจากมนุษยศาสตร์ โดยปล่อยให้วิทยาศาสตร์ธรรมชาติเป็นหน้าที่ของการวิเคราะห์ วิธีปฏิบัติ และภาษาที่แห้งแล้งของสูตรและตัวเลข คณิตศาสตร์ไม่สามารถจัดเป็นวิชามนุษยศาสตร์ได้ แต่หากไม่มีความคิดสร้างสรรค์คุณจะไม่ไปไกลใน "ราชินีแห่งวิทยาศาสตร์ทั้งหมด" - ผู้คนรู้จักสิ่งนี้มาเป็นเวลานาน ตั้งแต่สมัยพีทาโกรัส เป็นต้น

น่าเสียดายที่ตำราเรียนของโรงเรียนมักไม่ได้อธิบายว่าในวิชาคณิตศาสตร์ สิ่งสำคัญไม่เพียงแต่ต้องยัดเยียดทฤษฎีบท สัจพจน์ และสูตรเท่านั้น สิ่งสำคัญคือต้องเข้าใจและรู้สึกถึงหลักการพื้นฐานของมัน และในเวลาเดียวกันพยายามปลดปล่อยจิตใจของคุณจากความคิดโบราณและความจริงเบื้องต้น - เฉพาะในเงื่อนไขเช่นนี้เท่านั้นที่การค้นพบที่ยิ่งใหญ่จะเกิดขึ้นทั้งหมด

การค้นพบดังกล่าวรวมถึงสิ่งที่เรารู้ในปัจจุบันว่าเป็นทฤษฎีบทพีทาโกรัส ด้วยความช่วยเหลือนี้ เราจะพยายามแสดงให้เห็นว่าคณิตศาสตร์ไม่เพียงแต่สามารถทำได้ แต่ยังน่าตื่นเต้นอีกด้วย และการผจญภัยครั้งนี้ไม่เพียงเหมาะสำหรับเด็กเนิร์ดแว่นตาหนาเท่านั้น แต่ยังเหมาะสำหรับทุกคนที่มีจิตใจเข้มแข็งและจิตวิญญาณที่แข็งแกร่งอีกด้วย

จากประวัติความเป็นมาของปัญหา

พูดอย่างเคร่งครัด แม้ว่าทฤษฎีบทนี้จะเรียกว่า "ทฤษฎีบทพีทาโกรัส" แต่พีทาโกรัสเองก็ไม่ได้ค้นพบทฤษฎีบทนี้ สามเหลี่ยมมุมฉากและคุณสมบัติพิเศษของมันได้รับการศึกษามานานแล้ว มีมุมมองสองขั้วเกี่ยวกับปัญหานี้ ตามเวอร์ชันหนึ่ง พีทาโกรัสเป็นคนแรกที่ค้นพบข้อพิสูจน์ทฤษฎีบทที่สมบูรณ์ อีกประการหนึ่งหลักฐานไม่ได้เป็นของผู้ประพันธ์ของพีทาโกรัส

วันนี้คุณไม่สามารถตรวจสอบได้อีกต่อไปว่าใครถูกและใครผิด สิ่งที่ทราบก็คือข้อพิสูจน์ของพีทาโกรัส (หากเคยมีอยู่จริง) ก็ไม่รอด อย่างไรก็ตาม มีข้อเสนอแนะว่าข้อพิสูจน์ที่มีชื่อเสียงจาก Euclid's Elements อาจเป็นของ Pythagoras และ Euclid บันทึกไว้เท่านั้น

เป็นที่ทราบกันดีในปัจจุบันว่าปัญหาเกี่ยวกับสามเหลี่ยมมุมฉากพบได้ในแหล่งที่มาของอียิปต์ตั้งแต่สมัยฟาโรห์อาเมเนมฮัตที่ 1 บนแผ่นดินเหนียวของชาวบาบิโลนตั้งแต่รัชสมัยของกษัตริย์ฮัมมูราบีในตำราอินเดียโบราณ "Sulva Sutra" และงานของจีนโบราณ " โจวปี้ ซวนจิน”

อย่างที่คุณเห็น ทฤษฎีบทพีทาโกรัสครอบครองจิตใจของนักคณิตศาสตร์มาตั้งแต่สมัยโบราณ สิ่งนี้ได้รับการยืนยันด้วยหลักฐานต่าง ๆ ประมาณ 367 ชิ้นที่มีอยู่ในปัจจุบัน ในข้อนี้ไม่มีทฤษฎีบทอื่นใดสามารถแข่งขันกับทฤษฎีบทนี้ได้ ในบรรดานักเขียนบทพิสูจน์ที่มีชื่อเสียง เราสามารถระลึกถึง Leonardo da Vinci และ James Garfield ประธานาธิบดีคนที่ 20 ของสหรัฐอเมริกาได้ ทั้งหมดนี้พูดถึงความสำคัญอย่างยิ่งยวดของทฤษฎีบทนี้สำหรับคณิตศาสตร์: ทฤษฎีบทเรขาคณิตส่วนใหญ่ได้มาจากทฤษฎีบทนี้หรือมีความเชื่อมโยงกับทฤษฎีบทนี้ในทางใดทางหนึ่ง

การพิสูจน์ทฤษฎีบทพีทาโกรัส

หนังสือเรียนของโรงเรียนส่วนใหญ่จะให้ข้อพิสูจน์เกี่ยวกับพีชคณิต แต่แก่นแท้ของทฤษฎีบทนั้นอยู่ที่เรขาคณิต ดังนั้นก่อนอื่นเรามาพิจารณาข้อพิสูจน์ของทฤษฎีบทที่มีชื่อเสียงซึ่งมีพื้นฐานมาจากวิทยาศาสตร์นี้ก่อน

หลักฐานที่ 1

เพื่อการพิสูจน์ทฤษฎีบทพีทาโกรัสที่ง่ายที่สุดสำหรับสามเหลี่ยมมุมฉาก คุณต้องกำหนดเงื่อนไขในอุดมคติ: ปล่อยให้รูปสามเหลี่ยมไม่เพียงแต่เป็นมุมฉากเท่านั้น แต่ยังมีหน้าจั่วด้วย มีเหตุผลที่จะเชื่อได้ว่าสามเหลี่ยมชนิดนี้เป็นสิ่งที่นักคณิตศาสตร์โบราณพิจารณาในตอนแรก

คำแถลง “สี่เหลี่ยมจัตุรัสที่สร้างขึ้นบนด้านตรงข้ามมุมฉากของสามเหลี่ยมมุมฉากจะเท่ากับผลรวมของสี่เหลี่ยมจัตุรัสที่สร้างขึ้นบนขาของมัน”สามารถแสดงด้วยภาพวาดต่อไปนี้:

ดูสามเหลี่ยมหน้าจั่ว ABC: บนด้านตรงข้ามมุมฉาก AC คุณสามารถสร้างสี่เหลี่ยมจัตุรัสที่ประกอบด้วยสามเหลี่ยม 4 รูปซึ่งเท่ากับ ABC ดั้งเดิม และด้าน AB และ BC ก็มีการสร้างสี่เหลี่ยมจัตุรัสขึ้นมา แต่ละอันมีสามเหลี่ยมสองอันที่คล้ายกัน

อย่างไรก็ตาม ภาพวาดนี้เป็นพื้นฐานของเรื่องตลกและการ์ตูนมากมายที่อุทิศให้กับทฤษฎีบทพีทาโกรัส ที่มีชื่อเสียงที่สุดน่าจะเป็น “กางเกงพีทาโกรัสเท่าเทียมกันทุกทิศทุกทาง”:

หลักฐานที่ 2

วิธีการนี้เป็นการผสมผสานพีชคณิตและเรขาคณิตเข้าด้วยกัน และถือได้ว่าเป็นอีกวิธีหนึ่งของการพิสูจน์ Bhaskari นักคณิตศาสตร์ชาวอินเดียโบราณ

สร้างสามเหลี่ยมมุมฉากที่มีด้านข้าง ก ข และค(รูปที่ 1) จากนั้นสร้างสี่เหลี่ยมจัตุรัสสองอันโดยให้ด้านเท่ากับผลรวมของความยาวของขาทั้งสองข้าง - (ก+ข). ในแต่ละช่อง ให้ก่อสร้างดังรูปที่ 2 และ 3

ในสี่เหลี่ยมจัตุรัสแรก ให้สร้างสามเหลี่ยมสี่อันเหมือนกับในรูปที่ 1 ผลลัพธ์ที่ได้คือสี่เหลี่ยมสองอัน: อันหนึ่งมีด้าน a, อันที่สองมีด้าน ข.

ในสี่เหลี่ยมจัตุรัสที่สอง มีรูปสามเหลี่ยมที่คล้ายกันสี่รูปที่สร้างเป็นรูปสี่เหลี่ยมจัตุรัสซึ่งมีด้านเท่ากับด้านตรงข้ามมุมฉาก ค.

ผลรวมของพื้นที่ของสี่เหลี่ยมที่สร้างขึ้นในรูปที่ 2 เท่ากับพื้นที่ของสี่เหลี่ยมที่เราสร้างด้วยด้าน c ในรูปที่ 3 สามารถตรวจสอบได้ง่ายๆ ด้วยการคำนวณพื้นที่สี่เหลี่ยมในรูป 2 ตามสูตร และพื้นที่ของสี่เหลี่ยมจัตุรัสที่ถูกจารึกไว้ในรูปที่ 3 โดยการลบพื้นที่ของสามเหลี่ยมมุมฉากสี่รูปที่มีขนาดเท่ากันที่ถูกจารึกไว้ในสี่เหลี่ยมจัตุรัสออกจากพื้นที่ของสี่เหลี่ยมจัตุรัสขนาดใหญ่ที่มีด้าน (ก+ข).

การเขียนทั้งหมดนี้เรามี: ก 2 +ข 2 =(ก+ข) 2 – 2ab. เปิดวงเล็บ คำนวณพีชคณิตที่จำเป็นทั้งหมด แล้วรับสิ่งนั้น ก 2 +ข 2 = ก 2 +ข 2. ในกรณีนี้ พื้นที่ที่ถูกจารึกไว้ในรูปที่ 3 สี่เหลี่ยมจัตุรัสสามารถคำนวณได้โดยใช้สูตรดั้งเดิม ส=ค 2. เหล่านั้น. ก 2 +ข 2 =ค 2– คุณได้พิสูจน์ทฤษฎีบทพีทาโกรัสแล้ว

หลักฐานที่ 3

การพิสูจน์ของอินเดียโบราณนั้นอธิบายไว้ในศตวรรษที่ 12 ในบทความ "มงกุฎแห่งความรู้" (“ Siddhanta Shiromani”) และเป็นข้อโต้แย้งหลักที่ผู้เขียนใช้คำอุทธรณ์ที่ส่งถึงความสามารถทางคณิตศาสตร์และทักษะการสังเกตของนักเรียนและผู้ติดตาม: “ ดู!"

แต่เราจะวิเคราะห์หลักฐานนี้โดยละเอียด:

ภายในสี่เหลี่ยมจัตุรัส ให้สร้างสามเหลี่ยมมุมฉากสี่อันตามที่ระบุในภาพวาด ให้เราแสดงด้านของสี่เหลี่ยมจัตุรัสใหญ่หรือที่เรียกว่าด้านตรงข้ามมุมฉาก กับ. เรียกขาของสามเหลี่ยมกันดีกว่า กและ ข. ตามรูปวาด ด้านข้างของสี่เหลี่ยมด้านในคือ (ก-ข).

ใช้สูตรหาพื้นที่สี่เหลี่ยมจัตุรัส ส=ค 2เพื่อคำนวณพื้นที่ของสี่เหลี่ยมจัตุรัสด้านนอก และในเวลาเดียวกันก็คำนวณค่าเดียวกันโดยบวกพื้นที่ของสี่เหลี่ยมด้านในและพื้นที่ของสามเหลี่ยมมุมฉากทั้งสี่รูป: (ก-ข) 2 2+4*1\2*ก*ข.

คุณสามารถใช้ทั้งสองตัวเลือกในการคำนวณพื้นที่สี่เหลี่ยมเพื่อให้แน่ใจว่าผลลัพธ์เหมือนกัน และนี่ให้สิทธิ์คุณเขียนลงไป ค 2 =(ก-ข) 2 +4*1\2*ก*ข. จากผลของการแก้ปัญหา คุณจะได้สูตรของทฤษฎีบทพีทาโกรัส ค 2 =ก 2 +ข 2. ทฤษฎีบทได้รับการพิสูจน์แล้ว

หลักฐาน 4

หลักฐานจีนโบราณที่น่าสงสัยนี้ถูกเรียกว่า "เก้าอี้ของเจ้าสาว" - เนื่องจากรูปร่างที่เหมือนเก้าอี้ซึ่งเป็นผลมาจากการก่อสร้างทั้งหมด:

โดยจะใช้ภาพวาดที่เราได้เห็นแล้วในรูปที่ 3 ในการพิสูจน์ครั้งที่สอง และจัตุรัสด้านในที่มีด้าน c ถูกสร้างขึ้นในลักษณะเดียวกับหลักฐานอินเดียโบราณที่ให้ไว้ข้างต้น

หากคุณตัดสามเหลี่ยมสีเขียวสองอันออกจากภาพวาดในรูปที่ 1 ในใจ ให้ย้ายพวกมันไปที่ด้านตรงข้ามของสี่เหลี่ยมจัตุรัสด้วยด้าน c และแนบด้านตรงข้ามมุมฉากกับด้านตรงข้ามมุมฉากของสามเหลี่ยมไลแลค คุณจะได้ร่างที่เรียกว่า "เก้าอี้เจ้าสาว" (รูปที่ 2) เพื่อความชัดเจน คุณสามารถทำแบบเดียวกันกับกระดาษสี่เหลี่ยมและสามเหลี่ยมได้ คุณจะต้องแน่ใจว่า "เก้าอี้เจ้าสาว" นั้นประกอบด้วยสี่เหลี่ยมสองอัน: อันเล็กที่มีด้านข้าง ขและใหญ่มีด้านข้าง ก.

โครงสร้างเหล่านี้ทำให้นักคณิตศาสตร์ชาวจีนโบราณและเราติดตามพวกเขาได้ข้อสรุปว่า ค 2 =ก 2 +ข 2.

หลักฐานที่ 5

นี่เป็นอีกวิธีหนึ่งในการค้นหาคำตอบของทฤษฎีบทพีทาโกรัสโดยใช้เรขาคณิต เรียกว่าวิธีการ์ฟิลด์

สร้างสามเหลี่ยมมุมฉาก เอบีซี. เราจำเป็นต้องพิสูจน์ว่า ก่อนคริสต์ศักราช 2 = เอซี 2 + เอบี 2.

ในการทำเช่นนี้ให้ทำขาต่อ เครื่องปรับอากาศและสร้างส่วน ซีดีซึ่งเท่ากับขา เอบี. ลดแนวตั้งฉากลง ค.ศส่วนของเส้น ส.อ. เซ็กเมนต์ ส.อและ เครื่องปรับอากาศมีความเท่าเทียมกัน เชื่อมต่อจุดต่างๆ อีและ ใน, และ อีและ กับและรับภาพวาดตามภาพด้านล่าง:

เพื่อพิสูจน์หอคอยเราใช้วิธีที่เราได้ลองไปแล้วอีกครั้ง: เราค้นหาพื้นที่ของผลลัพธ์ที่ได้ในสองวิธีและแบ่งนิพจน์ให้กันและกัน

ค้นหาพื้นที่ของรูปหลายเหลี่ยม เตียงสามารถทำได้โดยการบวกพื้นที่ของสามเหลี่ยมทั้งสามที่ประกอบกันเป็นสามเหลี่ยมนั้น และหนึ่งในนั้น อีอาร์ยู, ไม่ใช่แค่สี่เหลี่ยมเท่านั้น แต่ยังมีหน้าจั่วอีกด้วย อย่าลืมสิ่งนั้นด้วย เอบี=ซีดี, เอซี=อีดีและ พ.ศ.=SE– สิ่งนี้จะทำให้เราสามารถลดความซับซ้อนของการบันทึกและไม่โอเวอร์โหลด ดังนั้น, S ABED =2*1/2(AB*AC)+1/2ВС 2.

ขณะเดียวกันก็เป็นที่ชัดเจนว่า เตียง- นี่คือสี่เหลี่ยมคางหมู ดังนั้นเราจึงคำนวณพื้นที่โดยใช้สูตร: ส เอเบด =(DE+AB)*1/2AD. สำหรับการคำนวณของเรา การแสดงกลุ่มจะสะดวกและชัดเจนยิ่งขึ้น ค.ศเป็นผลรวมของส่วนต่างๆ เครื่องปรับอากาศและ ซีดี.

มาเขียนทั้งสองวิธีในการคำนวณพื้นที่ของร่างโดยใส่เครื่องหมายเท่ากับระหว่างพวกเขา: AB*เอซี+1/2BC 2 =(DE+AB)*1/2(เอซี+ซีดี). เราใช้ความเท่าเทียมกันของกลุ่มที่เรารู้จักอยู่แล้วและอธิบายไว้ข้างต้นเพื่อทำให้ด้านขวาของสัญลักษณ์ง่ายขึ้น: AB*เอซี+1/2บีซี 2 =1/2(เอบี+เอซี) 2. ตอนนี้เรามาเปิดวงเล็บและแปลงความเท่าเทียมกัน: AB*เอซี+1/2บีซี 2 =1/2เอซี 2 +2*1/2(เอบี*เอซี)+1/2เอบี 2. เมื่อทำการเปลี่ยนแปลงทั้งหมดเสร็จแล้ว เราก็ได้สิ่งที่เราต้องการ: ก่อนคริสต์ศักราช 2 = เอซี 2 + เอบี 2. เราได้พิสูจน์ทฤษฎีบทแล้ว

แน่นอนว่ารายการหลักฐานนี้ยังห่างไกลจากความสมบูรณ์ ทฤษฎีบทพีทาโกรัสสามารถพิสูจน์ได้โดยใช้เวกเตอร์ จำนวนเชิงซ้อน สมการเชิงอนุพันธ์ สเตอริโอเมทรี ฯลฯ และแม้แต่นักฟิสิกส์: ตัวอย่างเช่นหากของเหลวถูกเทลงในปริมาตรสี่เหลี่ยมจัตุรัสและสามเหลี่ยมคล้ายกับที่แสดงในภาพวาด ด้วยการเทของเหลว คุณสามารถพิสูจน์ความเท่าเทียมกันของพื้นที่และทฤษฎีบทได้

คำไม่กี่คำเกี่ยวกับแฝดพีทาโกรัส

ประเด็นนี้มีน้อยหรือไม่มีการศึกษาเลยในหลักสูตรของโรงเรียน ในขณะเดียวกันก็น่าสนใจมากและมีความสำคัญอย่างยิ่งในเรขาคณิต ค่าสามเท่าของพีทาโกรัสใช้เพื่อแก้ปัญหาทางคณิตศาสตร์หลายอย่าง การทำความเข้าใจสิ่งเหล่านี้อาจเป็นประโยชน์กับคุณในการศึกษาต่อ

แล้วแฝดพีทาโกรัสคืออะไร? นี่คือชื่อของจำนวนธรรมชาติที่รวบรวมไว้เป็นกลุ่มสามกลุ่ม ผลรวมของกำลังสองของจำนวนนั้นเท่ากับจำนวนตัวที่สามยกกำลังสอง

ทริปเปิลพีทาโกรัสสามารถเป็น:

• ดั้งเดิม (ทั้งสามตัวเลขค่อนข้างเป็นจำนวนเฉพาะ);
• ไม่ใช่แบบดั้งเดิม (ถ้าแต่ละหมายเลขของ Triple คูณด้วยจำนวนเดียวกัน คุณจะได้ Triple ใหม่ซึ่งไม่ใช่แบบดั้งเดิม)

แม้กระทั่งก่อนยุคของเรา ชาวอียิปต์โบราณหลงใหลในความคลุ้มคลั่งในเรื่องจำนวนแฝดพีทาโกรัส: ในปัญหาพวกเขาถือว่าสามเหลี่ยมมุมฉากที่มีด้าน 3, 4 และ 5 หน่วย อย่างไรก็ตาม สามเหลี่ยมใดๆ ที่มีด้านเท่ากับตัวเลขจากสามเหลี่ยมพีทาโกรัสจะเป็นสี่เหลี่ยมตามค่าเริ่มต้น

ตัวอย่างของแฝดพีทาโกรัส: (3, 4, 5), (6, 8, 10), (5, 12, 13), (9, 12, 15), (8, 15, 17), (12, 16, 20 ), (15, 20, 25), (7, 24, 25), (10, 24, 26), (20, 21, 29), (18, 24, 30), (10, 30, 34) , (21, 28, 35), (12, 35, 37), (15, 36, 39), (24, 32, 40), (9, 40, 41), (27, 36, 45), ( 14 , 48, 50), (30, 40, 50) ฯลฯ

การประยุกต์ทฤษฎีบทในทางปฏิบัติ

ทฤษฎีบทพีทาโกรัสไม่เพียงแต่ใช้ในคณิตศาสตร์เท่านั้น แต่ยังใช้ในสถาปัตยกรรมและการก่อสร้าง ดาราศาสตร์ และแม้แต่วรรณคดีด้วย

ประการแรก เกี่ยวกับการก่อสร้าง: ทฤษฎีบทพีทาโกรัสถูกนำมาใช้กันอย่างแพร่หลายในปัญหาที่มีระดับความซับซ้อนต่างๆ ตัวอย่างเช่น ดูที่หน้าต่างแบบโรมาเนสก์:

ให้เราแสดงความกว้างของหน้าต่างเป็น ขจากนั้นรัศมีของครึ่งวงกลมหลักสามารถเขียนแทนได้ว่าเป็น รและแสดงออกผ่าน ข: R=ข/2. รัศมีของครึ่งวงกลมเล็กๆ ก็สามารถแสดงผ่านได้เช่นกัน ข: r=b/4. ในปัญหานี้ เราสนใจรัศมีของวงกลมด้านในของหน้าต่าง (เรียกอีกอย่างว่า พี).

ทฤษฎีบทพีทาโกรัสมีประโยชน์ในการคำนวณเท่านั้น ร. ในการทำเช่นนี้ เราใช้รูปสามเหลี่ยมมุมฉากซึ่งระบุด้วยเส้นประในรูป ด้านตรงข้ามมุมฉากของรูปสามเหลี่ยมประกอบด้วยสองรัศมี: ข/4+พี. ขาข้างหนึ่งแสดงถึงรัศมี ข/4, อื่น b/2-p. เราเขียนโดยใช้ทฤษฎีบทพีทาโกรัส: (b/4+p) 2 =(b/4) 2 +(b/2-p) 2. ต่อไปเราจะเปิดวงเล็บแล้วรับ ข 2 /16+ บีพี/2+พี 2 =ข 2 /16+ข 2 /4-bp+p 2. ลองแปลงนิพจน์นี้เป็น บีพี/2=บี 2 /4-bp. แล้วเราหารพจน์ทั้งหมดด้วย ขเรานำเสนอสิ่งที่คล้ายกันเพื่อรับ 3/2*พี=ข/4. และในที่สุดเราก็พบว่า พี=ข/6- ซึ่งเป็นสิ่งที่เราต้องการ

เมื่อใช้ทฤษฎีบท คุณสามารถคำนวณความยาวของจันทันสำหรับหลังคาหน้าจั่วได้ พิจารณาว่าต้องใช้เสาสื่อสารเคลื่อนที่สูงแค่ไหนเพื่อให้สัญญาณไปถึงพื้นที่ที่มีประชากรหนาแน่น และแม้กระทั่งติดตั้งต้นคริสต์มาสอย่างยั่งยืนในจัตุรัสกลางเมือง อย่างที่คุณเห็น ทฤษฎีบทนี้ไม่เพียงแต่อยู่บนหน้าหนังสือเรียนเท่านั้น แต่ยังมีประโยชน์ในชีวิตจริงอีกด้วย

ในวรรณคดี ทฤษฎีบทพีทาโกรัสเป็นแรงบันดาลใจให้นักเขียนมาตั้งแต่สมัยโบราณและยังคงเป็นเช่นนั้นในยุคของเรา ตัวอย่างเช่น Adelbert von Chamisso นักเขียนชาวเยอรมันในศตวรรษที่ 19 ได้รับแรงบันดาลใจให้เขียนโคลง:

แสงสว่างแห่งความจริงจะไม่ดับไปในเร็ววัน
แต่เมื่อส่องแสงแล้ว ก็ไม่น่าจะสลายไป
และเช่นเดียวกับเมื่อหลายพันปีก่อน
มันจะไม่ทำให้เกิดข้อสงสัยหรือข้อพิพาท

ฉลาดที่สุดเมื่อสัมผัสดวงตาของคุณ
แสงแห่งความจริง ขอบคุณพระเจ้า
และวัวหนึ่งร้อยตัวถูกฆ่าโกหก -
ของขวัญตอบแทนจากพีทาโกรัสผู้โชคดี

ตั้งแต่นั้นมาวัวก็คำรามอย่างสิ้นหวัง:
ทำให้ชนเผ่าวัวตื่นตระหนกตลอดไป
เหตุการณ์ที่กล่าวถึงที่นี่

ดูเหมือนว่าเวลานั้นกำลังจะมาถึงแล้ว
และพวกเขาจะเสียสละอีกครั้ง
ทฤษฎีบทที่ดีบางอย่าง

(แปลโดย Viktor Toporov)

และในศตวรรษที่ 20 Evgeny Veltistov นักเขียนชาวโซเวียตได้อุทิศทั้งบทในการพิสูจน์ทฤษฎีบทพีทาโกรัสในหนังสือของเขาเรื่อง The Adventures of Electronics และอีกครึ่งบทของเรื่องราวเกี่ยวกับโลกสองมิติที่อาจดำรงอยู่ได้หากทฤษฎีบทพีทาโกรัสกลายเป็นกฎพื้นฐานและแม้แต่ศาสนาสำหรับโลกใบเดียว การใช้ชีวิตที่นั่นจะง่ายกว่ามาก แต่ก็น่าเบื่อกว่ามากด้วย เช่น ไม่มีใครเข้าใจความหมายของคำว่า "กลม" และ "ปุย"

และในหนังสือ "The Adventures of Electronics" ผู้เขียนผ่านปากของครูคณิตศาสตร์ Taratar กล่าวว่า "สิ่งสำคัญในวิชาคณิตศาสตร์คือการเคลื่อนไหวของความคิด แนวคิดใหม่ ๆ" มันเป็นการหลีกหนีจากความคิดที่สร้างสรรค์อย่างแม่นยำซึ่งก่อให้เกิดทฤษฎีบทพีทาโกรัส - ไม่ใช่เพื่ออะไรที่มีข้อพิสูจน์ที่หลากหลายมากมาย ช่วยให้คุณก้าวข้ามขอบเขตของสิ่งที่คุ้นเคยและมองสิ่งที่คุ้นเคยในรูปแบบใหม่

บทสรุป

บทความนี้ถูกสร้างขึ้นเพื่อให้คุณสามารถมองข้ามหลักสูตรของโรงเรียนในวิชาคณิตศาสตร์และเรียนรู้ไม่เพียงแต่การพิสูจน์ทฤษฎีบทพีทาโกรัสที่ให้ไว้ในหนังสือเรียน "เรขาคณิต 7-9" (L.S. Atanasyan, V.N. Rudenko) และ "เรขาคณิต 7" - 11” (A.V. Pogorelov) แต่ยังมีวิธีอื่นที่น่าสนใจในการพิสูจน์ทฤษฎีบทที่มีชื่อเสียงอีกด้วย และยังดูตัวอย่างว่าทฤษฎีบทพีทาโกรัสสามารถนำไปใช้ในชีวิตประจำวันได้อย่างไร

ประการแรก ข้อมูลนี้จะช่วยให้คุณมีคุณสมบัติได้รับคะแนนที่สูงขึ้นในบทเรียนคณิตศาสตร์ - ข้อมูลเกี่ยวกับหัวข้อจากแหล่งข้อมูลเพิ่มเติมจะได้รับการชื่นชมอย่างสูงเสมอ

ประการที่สอง เราต้องการช่วยให้คุณรู้สึกว่าคณิตศาสตร์น่าสนใจเพียงใด ยืนยันด้วยตัวอย่างที่เฉพาะเจาะจงว่ามีพื้นที่สำหรับความคิดสร้างสรรค์อยู่เสมอ เราหวังว่าทฤษฎีบทพีทาโกรัสและบทความนี้จะเป็นแรงบันดาลใจให้คุณสำรวจและค้นพบสิ่งที่น่าตื่นเต้นในวิชาคณิตศาสตร์และวิทยาศาสตร์อื่นๆ อย่างอิสระ

บอกเราในความคิดเห็นหากคุณพบหลักฐานที่นำเสนอในบทความที่น่าสนใจ คุณพบว่าข้อมูลนี้มีประโยชน์ในการศึกษาของคุณหรือไม่? เขียนถึงเราว่าคุณคิดอย่างไรเกี่ยวกับทฤษฎีบทพีทาโกรัสและบทความนี้ - เรายินดีที่จะหารือทั้งหมดนี้กับคุณ

blog.site เมื่อคัดลอกเนื้อหาทั้งหมดหรือบางส่วน จำเป็นต้องมีลิงก์ไปยังแหล่งที่มาดั้งเดิม

(อ้างอิงจากปาปิรัส 6619 ของพิพิธภัณฑ์เบอร์ลิน) ตามคำกล่าวของคันทอร์ ฮาร์พีโดแนปต์หรือ "เครื่องดึงเชือก" ได้สร้างมุมฉากโดยใช้สามเหลี่ยมมุมฉากที่มีด้าน 3, 4 และ 5

มันง่ายมากที่จะทำซ้ำวิธีการก่อสร้าง ลองใช้เชือกยาว 12 ม. แล้วผูกแถบสีไว้ที่ระยะ 3 ม. จากปลายด้านหนึ่งและ 4 เมตรจากอีกด้านหนึ่ง มุมฉากจะอยู่ระหว่างด้านยาว 3 ถึง 4 เมตร ชาวฮาร์เปโดเนปเชียนอาจแย้งว่าวิธีการก่อสร้างของพวกเขากลายเป็นสิ่งฟุ่มเฟือยหากมีใครใช้ เช่น ไม้สี่เหลี่ยม ซึ่งช่างไม้ทุกคนใช้ แท้จริงแล้วภาพวาดของอียิปต์เป็นที่รู้จักกันดีซึ่งพบเครื่องมือดังกล่าวเช่นภาพวาดที่แสดงถึงการประชุมเชิงปฏิบัติการของช่างไม้

ค่อนข้างเป็นที่รู้จักมากขึ้นเกี่ยวกับทฤษฎีบทพีทาโกรัสในหมู่ชาวบาบิโลน ในข้อความหนึ่งย้อนหลังไปถึงสมัยฮัมมูราบีนั่นคือถึง 2,000 ปีก่อนคริสตกาล จ. จะได้รับการคำนวณโดยประมาณของด้านตรงข้ามมุมฉากของสามเหลี่ยมมุมฉาก จากนี้เราสามารถสรุปได้ว่าในเมโสโปเตเมียพวกเขาสามารถคำนวณด้วยสามเหลี่ยมมุมฉากได้อย่างน้อยก็ในบางกรณี ในด้านหนึ่ง จากระดับความรู้ปัจจุบันเกี่ยวกับคณิตศาสตร์อียิปต์และบาบิโลน และอีกด้านหนึ่ง จากการศึกษาเชิงวิพากษ์เกี่ยวกับแหล่งที่มาของกรีก Van der Waerden (นักคณิตศาสตร์ชาวดัตช์) สรุปว่ามีความเป็นไปได้สูงที่ ทฤษฎีบทเรื่องกำลังสองของด้านตรงข้ามมุมฉากเป็นที่รู้จักในอินเดียแล้วประมาณศตวรรษที่ 18 ก่อนคริสต์ศักราช จ.

ประมาณ 400 ปีก่อนคริสตกาล พ.ศ. ตามข้อมูลของ Proclus เพลโตได้ให้วิธีการค้นหาแฝดพีทาโกรัส โดยผสมผสานพีชคณิตและเรขาคณิตเข้าด้วยกัน ประมาณ 300 ปีก่อนคริสตกาล จ. ข้อพิสูจน์สัจพจน์ที่เก่าแก่ที่สุดของทฤษฎีบทพีทาโกรัสปรากฏในองค์ประกอบของยุคลิด

สูตร

สูตรทางเรขาคณิต:

ทฤษฎีบทถูกกำหนดไว้แต่เดิมดังนี้:

สูตรพีชคณิต:

นั่นคือ แสดงถึงความยาวของด้านตรงข้ามมุมฉากของรูปสามเหลี่ยมด้วย และความยาวของขาด้วย และ :

สูตรของทฤษฎีบททั้งสองสูตรมีค่าเท่ากัน แต่สูตรที่สองนั้นเป็นสูตรพื้นฐานมากกว่า ไม่ต้องการแนวคิดเรื่องพื้นที่ กล่าวคือ ข้อความที่สองสามารถตรวจสอบได้โดยไม่ต้องรู้อะไรเลยเกี่ยวกับพื้นที่ และโดยการวัดเฉพาะความยาวของด้านของสามเหลี่ยมมุมฉากเท่านั้น

ทฤษฎีบทคอนเวิร์สพีทาโกรัส:

การพิสูจน์

ในขณะนี้ มีการบันทึกข้อพิสูจน์ 367 ข้อเกี่ยวกับทฤษฎีบทนี้ในวรรณกรรมทางวิทยาศาสตร์ อาจเป็นไปได้ว่าทฤษฎีบทพีทาโกรัสอาจเป็นทฤษฎีบทเดียวที่มีการพิสูจน์จำนวนที่น่าประทับใจเช่นนี้ ความหลากหลายดังกล่าวสามารถอธิบายได้ด้วยความสำคัญพื้นฐานของทฤษฎีบทสำหรับเรขาคณิตเท่านั้น

แน่นอนว่าตามแนวคิดแล้วทั้งหมดสามารถแบ่งออกเป็นคลาสจำนวนเล็กน้อยได้ สิ่งที่มีชื่อเสียงที่สุด: การพิสูจน์โดยวิธีพื้นที่, การพิสูจน์ตามสัจพจน์และแปลกใหม่ (เช่น การใช้สมการเชิงอนุพันธ์)

ผ่านรูปสามเหลี่ยมที่คล้ายกัน

การพิสูจน์สูตรพีชคณิตต่อไปนี้เป็นการพิสูจน์ที่ง่ายที่สุด ซึ่งสร้างขึ้นจากสัจพจน์โดยตรง โดยเฉพาะอย่างยิ่งไม่ใช้แนวคิดเรื่องพื้นที่ของรูป

อนุญาต เอบีซีมีสามเหลี่ยมมุมฉากมีมุมฉาก ค. ลองวาดความสูงจาก คและแสดงฐานด้วย ชม. สามเหลี่ยม เอซีเอชคล้ายกับรูปสามเหลี่ยม เอบีซีตรงสองมุม สามเหลี่ยมเช่นเดียวกัน ซีบีเอชคล้ายกัน เอบีซี. โดยการแนะนำสัญกรณ์

เราได้รับ

สิ่งที่เทียบเท่า

เมื่อบวกกันแล้วเราก็จะได้

ซึ่งเป็นสิ่งที่จำเป็นต้องพิสูจน์

การพิสูจน์โดยใช้วิธีพื้นที่

ข้อพิสูจน์ด้านล่าง แม้จะดูเรียบง่าย แต่ก็ไม่ง่ายเลย พวกมันทั้งหมดใช้คุณสมบัติของพื้นที่ ซึ่งการพิสูจน์นั้นซับซ้อนกว่าการพิสูจน์ทฤษฎีบทพีทาโกรัสเสียอีก

พิสูจน์ผ่านการเสริมสมมูล

1. ลองจัดเรียงสามเหลี่ยมมุมฉากสี่อันเท่ากันดังแสดงในรูปที่ 1
2. สี่เหลี่ยมที่มีด้านข้าง คเป็นสี่เหลี่ยมจัตุรัส เนื่องจากผลรวมของมุมแหลมสองมุมคือ 90° และมุมตรงคือ 180°
3. ด้านหนึ่งมีพื้นที่ของรูปทั้งหมดเท่ากันกับพื้นที่ของสี่เหลี่ยมจัตุรัสที่มีด้าน (a + b) และอีกด้านหนึ่งเท่ากับผลรวมของพื้นที่ของสามเหลี่ยมทั้งสี่รูปและ พื้นที่ของสี่เหลี่ยมด้านใน

Q.E.D.

ข้อพิสูจน์ของยุคลิด

แนวคิดในการพิสูจน์ของ Euclid มีดังนี้ ลองพิสูจน์ว่าพื้นที่ครึ่งหนึ่งของสี่เหลี่ยมจัตุรัสที่สร้างขึ้นบนด้านตรงข้ามมุมฉากเท่ากับผลรวมของพื้นที่ครึ่งหนึ่งของสี่เหลี่ยมจัตุรัสที่สร้างบนขา และจากนั้นพื้นที่ของ สี่เหลี่ยมใหญ่และสี่เหลี่ยมเล็กสองอันมีค่าเท่ากัน

ลองดูภาพวาดทางด้านซ้าย บนนั้นเราสร้างสี่เหลี่ยมที่ด้านข้างของสามเหลี่ยมมุมฉากและดึงรังสี s จากจุดยอดของมุมฉาก C ซึ่งตั้งฉากกับด้านตรงข้ามมุมฉาก AB มันตัดสี่เหลี่ยม ABIK ที่สร้างขึ้นบนด้านตรงข้ามมุมฉากออกเป็นสี่เหลี่ยมสองอัน - BHJI และ HAKJ ตามลำดับ ปรากฎว่าพื้นที่ของสี่เหลี่ยมเหล่านี้เท่ากับพื้นที่สี่เหลี่ยมที่สร้างขึ้นบนขาที่สอดคล้องกันทุกประการ

ลองพิสูจน์ว่าพื้นที่ของสี่เหลี่ยม DECA เท่ากับพื้นที่ของสี่เหลี่ยม AHJK ในการทำเช่นนี้เราจะใช้การสังเกตเสริม: พื้นที่ของสามเหลี่ยมที่มีความสูงและฐานเท่ากับ สี่เหลี่ยมที่กำหนดมีค่าเท่ากับครึ่งหนึ่งของพื้นที่สี่เหลี่ยมที่กำหนด นี่เป็นผลมาจากการกำหนดพื้นที่ของสามเหลี่ยมเป็นครึ่งหนึ่งของผลคูณของฐานและความสูง จากการสังเกตนี้เป็นไปตามว่าพื้นที่ของสามเหลี่ยม ACK เท่ากับพื้นที่ของสามเหลี่ยม AHK (ไม่แสดงในรูป) ซึ่งจะเท่ากับครึ่งหนึ่งของพื้นที่สี่เหลี่ยม AHJK

ตอนนี้ให้เราพิสูจน์ว่าพื้นที่ของสามเหลี่ยม ACK เท่ากับครึ่งหนึ่งของพื้นที่ DECA สี่เหลี่ยมจัตุรัสด้วย สิ่งเดียวที่ต้องทำเพื่อสิ่งนี้คือการพิสูจน์ความเท่าเทียมกันของสามเหลี่ยม ACK และ BDA (เนื่องจากพื้นที่ของสามเหลี่ยม BDA เท่ากับครึ่งหนึ่งของพื้นที่ของสี่เหลี่ยมตามคุณสมบัติข้างต้น) ความเท่าเทียมกันนี้ชัดเจน: สามเหลี่ยมทั้งสองข้างเท่ากันและมีมุมระหว่างสามเหลี่ยมเหล่านั้น กล่าวคือ - AB=AK, AD=AC - ความเท่าเทียมกันของมุม CAK และ BAD นั้นพิสูจน์ได้ง่ายโดยวิธีการเคลื่อนที่: เราหมุนสามเหลี่ยม CAK 90° ทวนเข็มนาฬิกา จากนั้นจะเห็นได้ชัดว่าด้านที่สอดคล้องกันของสามเหลี่ยมทั้งสองใน คำถามจะตรงกัน (เนื่องจากมุมที่จุดยอดของรูปสี่เหลี่ยมจัตุรัสคือ 90°)

เหตุผลสำหรับความเท่าเทียมกันของพื้นที่ของสี่เหลี่ยมจัตุรัส BCFG และสี่เหลี่ยม BHJI นั้นคล้ายกันโดยสิ้นเชิง

ดังนั้นเราจึงพิสูจน์ว่าพื้นที่ของสี่เหลี่ยมจัตุรัสที่สร้างขึ้นบนด้านตรงข้ามมุมฉากนั้นประกอบด้วยพื้นที่สี่เหลี่ยมจัตุรัสที่สร้างขึ้นบนขา แนวคิดเบื้องหลังข้อพิสูจน์นี้แสดงให้เห็นเพิ่มเติมจากภาพเคลื่อนไหวด้านบน

หลักฐานของเลโอนาร์โด ดา วินชี

องค์ประกอบหลักของการพิสูจน์คือความสมมาตรและการเคลื่อนที่

ลองพิจารณาภาพวาดดังที่เห็นได้จากความสมมาตร ส่วนจะตัดสี่เหลี่ยมจัตุรัสออกเป็นสองส่วนที่เหมือนกัน (เนื่องจากสามเหลี่ยมมีความเท่ากันในการก่อสร้าง)

เมื่อใช้การหมุนทวนเข็มนาฬิกา 90 องศาไปรอบๆ จุด เราจะเห็นความเท่าเทียมกันของตัวเลขที่แรเงาและ

ตอนนี้เห็นได้ชัดว่าพื้นที่ของร่างที่เราแรเงานั้นเท่ากับผลรวมของครึ่งหนึ่งของพื้นที่สี่เหลี่ยมเล็ก ๆ (สร้างบนขา) และพื้นที่ของสามเหลี่ยมดั้งเดิม ในทางกลับกัน จะเท่ากับครึ่งหนึ่งของพื้นที่ของสี่เหลี่ยมจัตุรัสขนาดใหญ่ (สร้างจากด้านตรงข้ามมุมฉาก) บวกกับพื้นที่ของสามเหลี่ยมเดิม ดังนั้น ผลรวมครึ่งหนึ่งของพื้นที่ของสี่เหลี่ยมจัตุรัสเล็กจะเท่ากับครึ่งหนึ่งของพื้นที่ของสี่เหลี่ยมจัตุรัสขนาดใหญ่ ดังนั้น ผลรวมของพื้นที่สี่เหลี่ยมจัตุรัสที่สร้างบนขาจึงเท่ากับพื้นที่ของสี่เหลี่ยมจัตุรัสที่สร้างบน ด้านตรงข้ามมุมฉาก

พิสูจน์ด้วยวิธีขั้นต่ำสุด

การพิสูจน์โดยใช้สมการเชิงอนุพันธ์ต่อไปนี้มักมาจากนักคณิตศาสตร์ชาวอังกฤษชื่อดัง Hardy ซึ่งอาศัยอยู่ในช่วงครึ่งแรกของศตวรรษที่ 20

ดูภาพวาดที่แสดงในภาพและสังเกตการเปลี่ยนแปลงด้านข้าง กเราสามารถเขียนความสัมพันธ์ต่อไปนี้สำหรับการเพิ่มขึ้นทีละน้อยได้ กับและ ก(ใช้ความคล้ายคลึงกันของสามเหลี่ยม):

เราพบว่าใช้วิธีการแยกตัวแปร

นิพจน์ทั่วไปสำหรับการเปลี่ยนแปลงด้านตรงข้ามมุมฉากในกรณีที่เพิ่มขึ้นทั้งสองด้าน

เราได้รับการรวมสมการนี้และการใช้เงื่อนไขเริ่มต้น

เราจึงได้คำตอบที่ต้องการ

ตามที่เห็นได้ง่าย การพึ่งพากำลังสองในสูตรสุดท้ายปรากฏขึ้นเนื่องจากสัดส่วนเชิงเส้นระหว่างด้านข้างของรูปสามเหลี่ยมกับส่วนที่เพิ่มขึ้น ในขณะที่ผลรวมสัมพันธ์กับส่วนที่เพิ่มขึ้นอย่างอิสระจากการเพิ่มขึ้นของขาต่างๆ

สามารถหาข้อพิสูจน์ที่ง่ายกว่านี้ได้หากเราถือว่าขาข้างใดข้างหนึ่งไม่มีส่วนเพิ่มขึ้น (ในกรณีนี้คือขา) จากนั้นสำหรับค่าคงที่อินทิเกรตที่เราได้รับ

รูปแบบและลักษณะทั่วไป

รูปทรงเรขาคณิตที่คล้ายกันทั้งสามด้าน

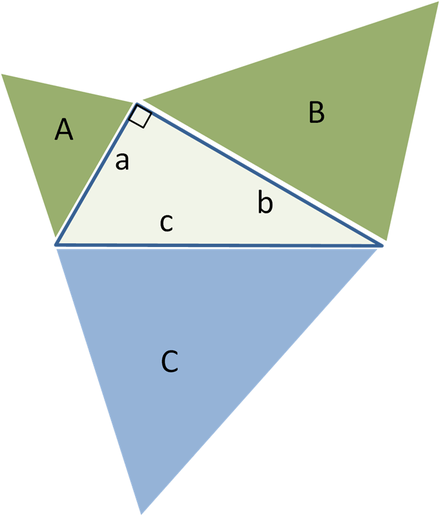
ลักษณะทั่วไปของสามเหลี่ยมที่คล้ายกัน พื้นที่รูปทรงสีเขียว A + B = พื้นที่สีน้ำเงิน C

ทฤษฎีบทพีทาโกรัสโดยใช้สามเหลี่ยมมุมฉากที่คล้ายกัน

ยุคลิดได้สรุปทฤษฎีบทพีทาโกรัสในงานของเขา จุดเริ่มต้นโดยขยายพื้นที่ของสี่เหลี่ยมจัตุรัสด้านข้างไปยังพื้นที่ของรูปทรงเรขาคณิตที่คล้ายกัน:

หากเราสร้างรูปทรงเรขาคณิตที่คล้ายกัน (ดูเรขาคณิตแบบยุคลิด) ที่ด้านข้างของสามเหลี่ยมมุมฉาก ผลรวมของตัวเลขที่เล็กกว่าทั้งสองจะเท่ากับพื้นที่ของรูปที่ใหญ่กว่า

แนวคิดหลักของการวางนัยทั่วไปนี้คือพื้นที่ของรูปทรงเรขาคณิตนั้นเป็นสัดส่วนกับกำลังสองของมิติเชิงเส้นใด ๆ และโดยเฉพาะกับกำลังสองของความยาวของด้านใด ๆ ดังนั้นสำหรับตัวเลขที่คล้ายกันกับพื้นที่ ก, บีและ คสร้างขึ้นด้านข้างที่มีความยาว ก, ขและ ค, เรามี:

แต่ตามทฤษฎีบทพีทาโกรัส ก 2 + ข 2 = ค 2 แล้ว ก + บี = ค.

ในทางกลับกันถ้าเราสามารถพิสูจน์ได้ว่า ก + บี = คสำหรับรูปทรงเรขาคณิตสามตัวที่คล้ายกันโดยไม่ต้องใช้ทฤษฎีบทพีทาโกรัส เราก็สามารถพิสูจน์ทฤษฎีบทนั้นได้ โดยเคลื่อนที่ไปในทิศทางตรงกันข้าม ตัวอย่างเช่น สามเหลี่ยมศูนย์กลางเริ่มต้นสามารถนำมาใช้ซ้ำเป็นรูปสามเหลี่ยมได้ คบนด้านตรงข้ามมุมฉาก และสามเหลี่ยมมุมฉากสองอันที่คล้ายกัน ( กและ บี) สร้างขึ้นบนอีกสองด้านซึ่งเกิดจากการหารสามเหลี่ยมตรงกลางด้วยความสูง ผลรวมของพื้นที่สามเหลี่ยมเล็กทั้งสองจะเท่ากับพื้นที่ของสามเหลี่ยมที่สามอย่างเห็นได้ชัด ก + บี = คและจากการพิสูจน์ก่อนหน้าในลำดับย้อนกลับ เราจะได้ทฤษฎีบทพีทาโกรัส a 2 + b 2 = c 2

ทฤษฎีบทโคไซน์

ทฤษฎีบทพีทาโกรัสเป็นกรณีพิเศษของทฤษฎีบทโคไซน์ทั่วไป ซึ่งสัมพันธ์กับความยาวของด้านในรูปสามเหลี่ยมใดๆ ก็ตาม:

โดยที่ θ คือมุมระหว่างด้าน กและ ข.

ถ้า θ เท่ากับ 90 องศา แล้ว cos θ = 0 และสูตรลดรูปลงตามทฤษฎีบทพีทาโกรัสปกติ

สามเหลี่ยมฟรี

ไปยังมุมที่เลือกของสามเหลี่ยมใดก็ได้ที่มีด้านข้าง ก ข คขอให้เราเขียนสามเหลี่ยมหน้าจั่วในลักษณะที่มุมที่เท่ากันที่ฐาน θ เท่ากับมุมที่เลือก สมมติว่ามุมที่เลือก θ อยู่ตรงข้ามด้านที่กำหนด ค. ผลลัพธ์ที่ได้คือสามเหลี่ยม ABD ที่มีมุม θ ซึ่งตั้งอยู่ตรงข้ามด้านข้าง กและงานปาร์ตี้ ร. รูปสามเหลี่ยมอันที่สองประกอบด้วยมุม θ ซึ่งตั้งอยู่ตรงข้ามด้านข้าง ขและงานปาร์ตี้ กับความยาว สดังที่แสดงในภาพ ซะบิต อิบนุ กุรเราะห์แย้งว่าด้านต่างๆ ของสามเหลี่ยมทั้งสามนี้มีความสัมพันธ์กันดังนี้:

เมื่อมุม θ เข้าใกล้ π/2 ฐานของสามเหลี่ยมหน้าจั่วจะเล็กลง และด้านทั้งสอง r และ s เหลื่อมกันน้อยลงเรื่อยๆ เมื่อ θ = π/2, ADB จะกลายเป็นสามเหลี่ยมมุมฉาก ร + ส = คและเราได้ทฤษฎีบทพีทาโกรัสตั้งต้น

ลองพิจารณาข้อโต้แย้งข้อหนึ่ง สามเหลี่ยม ABC มีมุมเดียวกันกับสามเหลี่ยม ABD แต่กลับกัน (สามเหลี่ยมทั้งสองมีมุมร่วมกันที่จุดยอด B ทั้งสองมีมุม θ และยังมีมุมที่สามเหมือนกัน ขึ้นอยู่กับผลรวมของมุมของสามเหลี่ยม) ดังนั้น ABC จึงคล้ายกับการสะท้อน ABD ของสามเหลี่ยม DBA ดังที่ แสดงในรูปด้านล่าง ให้เราเขียนความสัมพันธ์ระหว่างด้านตรงข้ามกับด้านที่อยู่ติดกับมุม θ

ภาพสะท้อนของสามเหลี่ยมอีกอันหนึ่งด้วย

ลองคูณเศษส่วนและเพิ่มอัตราส่วนทั้งสองนี้:

Q.E.D.

ลักษณะทั่วไปของรูปสามเหลี่ยมตามอำเภอใจผ่านรูปสี่เหลี่ยมด้านขนาน

ลักษณะทั่วไปของรูปสามเหลี่ยมโดยพลการ
พื้นที่สีเขียว พล็อต = พื้นที่สีฟ้า

หลักฐานวิทยานิพนธ์ในรูปด้านบนนี้

เรามาอธิบายลักษณะทั่วไปเพิ่มเติมสำหรับสามเหลี่ยมที่ไม่ใช่สามเหลี่ยมโดยใช้รูปสี่เหลี่ยมด้านขนานทั้งสามด้านแทนสี่เหลี่ยมจัตุรัส (รูปสี่เหลี่ยมด้านขนานเป็นกรณีพิเศษ) รูปบนแสดงว่าสำหรับรูปสามเหลี่ยมมุมแหลม พื้นที่ของรูปสี่เหลี่ยมด้านขนานด้านยาวเท่ากับผลรวมของรูปสี่เหลี่ยมด้านขนานที่อยู่อีกสองด้านที่เหลือ โดยมีเงื่อนไขว่ารูปสี่เหลี่ยมด้านขนานด้านยาว ด้านข้างถูกสร้างขึ้นตามที่แสดงในภาพ (ขนาดที่ระบุโดยลูกศรจะเท่ากันและกำหนดด้านของสี่เหลี่ยมด้านขนานล่าง) การแทนที่สี่เหลี่ยมจัตุรัสด้วยสี่เหลี่ยมด้านขนานนี้มีความคล้ายคลึงอย่างชัดเจนกับทฤษฎีบทเริ่มต้นของพีทาโกรัส ซึ่งคิดว่าได้รับการคิดค้นโดย Pappus แห่งอเล็กซานเดรียในคริสตศักราชที่ 4 จ.

รูปล่างแสดงความคืบหน้าของการพิสูจน์ ลองดูที่ด้านซ้ายของสามเหลี่ยม สี่เหลี่ยมด้านขนานสีเขียวด้านซ้ายมีพื้นที่เดียวกับด้านซ้ายของสี่เหลี่ยมด้านขนานสีน้ำเงินเนื่องจากมีฐานเท่ากัน ขและความสูง ชม.. นอกจากนี้ สี่เหลี่ยมด้านขนานสีเขียวด้านซ้ายยังมีพื้นที่เดียวกับสี่เหลี่ยมด้านขนานสีเขียวด้านซ้ายในภาพด้านบน เนื่องจากมีฐานร่วมกัน (ด้านซ้ายบนของรูปสามเหลี่ยม) และมีความสูงร่วมตั้งฉากกับด้านนั้นของรูปสามเหลี่ยม เมื่อใช้เหตุผลที่คล้ายกันสำหรับด้านขวาของสามเหลี่ยม เราจะพิสูจน์ว่าสี่เหลี่ยมด้านขนานล่างมีพื้นที่เดียวกันกับสี่เหลี่ยมด้านขนานสีเขียวสองอัน

จำนวนเชิงซ้อน

ทฤษฎีบทพีทาโกรัสใช้เพื่อค้นหาระยะห่างระหว่างจุดสองจุดในระบบพิกัดคาร์ทีเซียน และทฤษฎีบทนี้ใช้ได้กับพิกัดจริงทั้งหมด: ระยะทาง สระหว่างสองจุด ( ก, ข) และ ( ซีดี) เท่ากับ

สูตรจะไม่มีปัญหาหากถือว่าจำนวนเชิงซ้อนเป็นเวกเตอร์ที่มีส่วนประกอบจริง x + ฉันใช่ = (x, ย). . เช่น ระยะทาง สระหว่าง 0 + 1 ฉันและ 1 + 0 ฉันคำนวณเป็นโมดูลัสของเวกเตอร์ (0, 1) − (1, 0) = (−1, 1), หรือ

อย่างไรก็ตาม สำหรับการทำงานกับเวกเตอร์ที่มีพิกัดเชิงซ้อน จำเป็นต้องปรับปรุงสูตรพีทาโกรัสบางประการ ระยะห่างระหว่างจุดที่มีจำนวนเชิงซ้อน ( ก, ข) และ ( ค, ง); ก, ข, ค, และ งซับซ้อนทั้งหมด เรากำหนดโดยใช้ค่าสัมบูรณ์ ระยะทาง สขึ้นอยู่กับผลต่างเวกเตอร์ (ก − ค, ข − ง) ในรูปแบบต่อไปนี้: ปล่อยให้ความแตกต่าง ก − ค = พี+ฉัน ถาม, ที่ไหน พี- ส่วนที่แท้จริงของความแตกต่าง ถามคือส่วนจินตภาพ และ i = √(−1) ในทำนองเดียวกันให้ ข − ง = ร+ฉัน ส. แล้ว:

โดยที่หมายเลขคอนจูเกตเชิงซ้อนของ เช่น ระยะห่างระหว่างจุด (ก, ข) = (0, 1) และ (ค, ง) = (ฉัน, 0) ลองคำนวณความแตกต่างกัน (ก − ค, ข − ง) = (−ฉัน, 1) และผลลัพธ์จะเป็น 0 หากไม่ได้ใช้คอนจูเกตที่ซับซ้อน ดังนั้นเราจึงได้สูตรที่ปรับปรุงแล้ว

โมดูลถูกกำหนดดังนี้:

สเตอริโอเมทรี

ลักษณะทั่วไปที่สำคัญของทฤษฎีบทพีทาโกรัสสำหรับปริภูมิสามมิติคือทฤษฎีบทของเดอกอย ซึ่งตั้งชื่อตาม J.-P de Gois: หากจัตุรมุขมีมุมฉาก (เช่นในลูกบาศก์) ดังนั้นพื้นที่สี่เหลี่ยมจัตุรัสของใบหน้าที่อยู่ตรงข้ามมุมขวาจะเท่ากับผลรวมของกำลังสองของพื้นที่ของอีกสามใบหน้า ข้อสรุปนี้สามารถสรุปได้ว่า " n-มิติทฤษฎีบทพีทาโกรัส":

ทฤษฎีบทพีทาโกรัสในปริภูมิสามมิติเชื่อมโยง AD ในแนวทแยงกับด้านทั้งสาม

ลักษณะทั่วไปอีกประการหนึ่ง: ทฤษฎีบทพีทาโกรัสสามารถนำไปใช้กับสามมิติได้ในรูปแบบต่อไปนี้ พิจารณาสี่เหลี่ยมด้านขนานดังแสดงในรูป ลองหาความยาวของเส้นทแยงมุม BD โดยใช้ทฤษฎีบทพีทาโกรัส:

โดยที่ด้านทั้งสามประกอบกันเป็นรูปสามเหลี่ยมมุมฉาก เราใช้เส้นทแยงมุมแนวนอน BD และขอบแนวตั้ง AB เพื่อค้นหาความยาวของเส้นทแยงมุม AD ในกรณีนี้ เราใช้ทฤษฎีบทพีทาโกรัสอีกครั้ง:

หรือถ้าเราเขียนทุกอย่างไว้ในสมการเดียว:

ผลลัพธ์นี้คือนิพจน์สามมิติสำหรับกำหนดขนาดของเวกเตอร์ โวลต์(AD แนวทแยง) แสดงในรูปขององค์ประกอบตั้งฉาก ( โวลต์ k ) (สามด้านตั้งฉากกัน):

สมการนี้ถือได้ว่าเป็นลักษณะทั่วไปของทฤษฎีบทพีทาโกรัสสำหรับปริภูมิหลายมิติ อย่างไรก็ตาม ผลลัพธ์ที่ได้คือการประยุกต์ใช้ทฤษฎีบทพีทาโกรัสซ้ำๆ กับลำดับของสามเหลี่ยมมุมฉากในระนาบตั้งฉากต่อเนื่องกัน

พื้นที่เวกเตอร์

ในกรณีของระบบเวกเตอร์ตั้งฉาก มีความเท่าเทียมกัน ซึ่งเรียกอีกอย่างว่าทฤษฎีบทพีทาโกรัส:

ถ้า - นี่คือเส้นโครงของเวกเตอร์บนแกนพิกัด สูตรนี้เกิดขึ้นพร้อมกับระยะแบบยุคลิด - และหมายความว่าความยาวของเวกเตอร์เท่ากับรากที่สองของผลรวมของกำลังสองของส่วนประกอบต่างๆ

ความคล้ายคลึงของความเท่าเทียมกันนี้ในกรณีของระบบเวกเตอร์ที่ไม่มีที่สิ้นสุดเรียกว่าความเท่าเทียมกันของพาร์เซวัล

เรขาคณิตที่ไม่ใช่แบบยุคลิด

ทฤษฎีบทพีทาโกรัสได้มาจากสัจพจน์ของเรขาคณิตแบบยุคลิด และอันที่จริงแล้ว ใช้ไม่ได้กับเรขาคณิตที่ไม่ใช่แบบยุคลิด ในรูปแบบที่เขียนไว้ข้างต้น (นั่นคือ ทฤษฎีบทพีทาโกรัสกลายเป็นแบบหนึ่งที่เทียบเท่ากับสมมุติฐานของความเท่าเทียมของยุคลิด) กล่าวอีกนัยหนึ่ง ในเรขาคณิตที่ไม่ใช่แบบยุคลิด ความสัมพันธ์ระหว่างด้านของสามเหลี่ยมจะต้องอยู่ในรูปแบบที่แตกต่างจากทฤษฎีบทของพีทาโกรัส ตัวอย่างเช่น ในเรขาคณิตทรงกลม ด้านทั้งสามของสามเหลี่ยมมุมฉาก (เช่น ก, ขและ ค) ซึ่งจำกัดค่าออกแทนต์ (ส่วนที่แปด) ของทรงกลมหนึ่งหน่วย จะมีความยาว π/2 ซึ่งขัดแย้งกับทฤษฎีบทพีทาโกรัส เนื่องจาก ก 2 + ข 2 ≠ ค 2 .

ให้เราพิจารณาสองกรณีของเรขาคณิตที่ไม่ใช่แบบยุคลิด ได้แก่ เรขาคณิตทรงกลมและเรขาคณิตไฮเปอร์โบลิก ในทั้งสองกรณี สำหรับปริภูมิแบบยุคลิดสำหรับสามเหลี่ยมมุมฉาก ผลลัพธ์ซึ่งมาแทนที่ทฤษฎีบทพีทาโกรัสจะตามมาด้วยทฤษฎีบทโคไซน์

อย่างไรก็ตาม ทฤษฎีบทพีทาโกรัสยังคงใช้ได้สำหรับเรขาคณิตไฮเปอร์โบลิกและวงรี หากข้อกำหนดที่ว่าสามเหลี่ยมเป็นรูปสี่เหลี่ยมผืนผ้าถูกแทนที่ด้วยเงื่อนไขที่ว่าผลรวมของสองมุมของสามเหลี่ยมจะต้องเท่ากับมุมที่สาม กล่าวคือ ก+บี = ค. จากนั้นความสัมพันธ์ระหว่างด้านจะเป็นดังนี้ ผลรวมของพื้นที่วงกลมที่มีเส้นผ่านศูนย์กลาง กและ ขเท่ากับพื้นที่ของวงกลมที่มีเส้นผ่านศูนย์กลาง ค.

เรขาคณิตทรงกลม

สำหรับสามเหลี่ยมมุมฉากใดๆ บนทรงกลมที่มีรัศมี ร(เช่น ถ้ามุม γ ในรูปสามเหลี่ยมอยู่ทางขวา) กับด้าน ก, ข, คความสัมพันธ์ระหว่างทั้งสองฝ่ายจะมีลักษณะดังนี้:

ความเท่าเทียมกันนี้สามารถหาได้เป็นกรณีพิเศษของทฤษฎีบทโคไซน์ทรงกลม ซึ่งใช้ได้กับรูปสามเหลี่ยมทรงกลมทั้งหมด:

โดยที่ cosh คือโคไซน์ไฮเปอร์โบลิก สูตรนี้เป็นกรณีพิเศษของทฤษฎีบทไฮเปอร์โบลิกโคไซน์ ซึ่งใช้ได้กับรูปสามเหลี่ยมทุกรูป:

โดยที่ γ คือมุมที่มีจุดยอดอยู่ตรงข้ามกับด้าน ค.

ที่ไหน ก ฉันเรียกว่าเมตริกเทนเซอร์ อาจเป็นหน้าที่ของตำแหน่ง ช่องว่างโค้งดังกล่าวรวมถึงเรขาคณิตแบบรีแมนเนียนเป็นตัวอย่างทั่วไป สูตรนี้ยังเหมาะสำหรับปริภูมิแบบยุคลิดเมื่อใช้พิกัดเส้นโค้ง ตัวอย่างเช่น สำหรับพิกัดเชิงขั้ว:

งานศิลปะของเว็กเตอร์

ทฤษฎีบทพีทาโกรัสเชื่อมโยงสองนิพจน์สำหรับขนาดของผลคูณเวกเตอร์ วิธีหนึ่งในการกำหนดผลคูณไขว้นั้นต้องการให้เป็นไปตามสมการ:

สูตรนี้ใช้ผลคูณดอท ทางด้านขวาของสมการเรียกว่าตัวกำหนดแกรมสำหรับ กและ ขซึ่งเท่ากับพื้นที่ของสี่เหลี่ยมด้านขนานที่เกิดจากเวกเตอร์สองตัวนี้ ขึ้นอยู่กับข้อกำหนดนี้ เช่นเดียวกับข้อกำหนดที่ว่าผลิตภัณฑ์เวกเตอร์ตั้งฉากกับส่วนประกอบต่างๆ กและ ขตามนั้น ยกเว้นกรณีเล็กๆ น้อยๆ จากปริภูมิ 0 และ 1 มิติ ผลคูณไขว้ถูกกำหนดไว้เฉพาะในสามมิติและเจ็ดเท่านั้น เราใช้นิยามของมุมใน n- พื้นที่มิติ:

คุณสมบัติของผลคูณไขว้นี้ให้ขนาดดังนี้:

ด้วยอัตลักษณ์ตรีโกณมิติพื้นฐานของพีทาโกรัส เราได้รูปแบบการเขียนค่าของมันอีกรูปแบบหนึ่ง:

อีกวิธีหนึ่งในการกำหนดผลคูณไขว้คือการใช้นิพจน์สำหรับขนาด จากนั้น เมื่อให้เหตุผลในลำดับย้อนกลับ เราจะได้ความสัมพันธ์กับผลคูณสเกลาร์:

ดูสิ่งนี้ด้วย

หมายเหตุ

1. หัวข้อประวัติศาสตร์: ทฤษฎีบทของปีทาโกรัสในคณิตศาสตร์บาบิโลน
2. ( , หน้า 351) หน้า 351
3. ( , เล่มที่ 1, หน้า 144)
4. การอภิปรายข้อเท็จจริงทางประวัติศาสตร์มีอยู่ใน (หน้า 351) หน้า 351
5. เคิร์ต วอน ฟริตซ์ (เม.ย., 1945) "การค้นพบความไม่สมดุลโดยฮิปปาซัสแห่งเมตาปอนตัม" พงศาวดารของคณิตศาสตร์ ชุดที่สอง(พงศาวดารคณิตศาสตร์) 46 (2): 242–264.
6. Lewis Carroll, “The Story with Knots”, M., Mir, 1985, p. 7
7. แอสเกอร์ อาโบเรื่องราวจากประวัติศาสตร์คณิตศาสตร์ยุคแรกเริ่ม - สมาคมคณิตศาสตร์แห่งอเมริกา, 2540 - หน้า 51. - ISBN 0883856131
8. ข้อเสนอหลามโดย เอลีชา สก็อตต์ ลูมิส
9. ยุคลิด องค์ประกอบ: เล่มที่ 6 ข้อเสนอ VI 31: “ในรูปสามเหลี่ยมมุมฉาก รูปที่อยู่ด้านข้างซึ่งยื่นออกมาจากมุมฉากจะเท่ากับรูปที่คล้ายกันและอธิบายในทำนองเดียวกันที่อยู่ด้านข้างซึ่งมีมุมฉาก”
10. ลอว์เรนซ์ เอส. เลฟฟ์ อ้างถึงงาน. - ชุดการศึกษาของบาร์รอน - หน้า 326. - ISBN 0764128922
11. ฮาวเวิร์ด วิทลีย์ อีฟส์§4.8:...ภาพรวมของทฤษฎีบทพีทาโกรัส // ช่วงเวลาที่ยิ่งใหญ่ทางคณิตศาสตร์ (ก่อนปี 1650) - สมาคมคณิตศาสตร์แห่งอเมริกา, 2526. - หน้า 41. - ISBN 0883853108
12. ฏอบิท บิน กอร์รา (ชื่อเต็ม ธาบิท บิน กุรรา บิน มัรวัน อัล-Ṣābiʾ อัล-ฮารานี) (ค.ศ. 826-901) เป็นแพทย์ที่อาศัยอยู่ในแบกแดด ผู้เขียนบทความอย่างกว้างขวางเกี่ยวกับองค์ประกอบของยุคลิดและวิชาคณิตศาสตร์อื่นๆ
13. อัยดิน ซายลี (มี.ค. 1960) ฐาบิต อิบนุ กุรเราะห์สรุปทฤษฎีบทพีทาโกรัสโดยสรุป ไอซิส 51 (1): 35–37. ดอย:10.1086/348837.
14. จูดิธ ดี. แซลลี่, พอล แซลลี่แบบฝึกหัด 2.10 (ii) // อ้างถึงงาน - ป. 62. - ISBN 0821844032
15. ดูรายละเอียดการก่อสร้างดังกล่าวได้ที่ จอร์จ เจนนิงส์รูปที่ 1.32: ทฤษฎีบทพีทาโกรัสทั่วไป // เรขาคณิตสมัยใหม่พร้อมการใช้งาน: มี 150 หลัก - ที่ 3 - สปริงเกอร์, 1997. - หน้า 23. - ISBN 038794222X
16. อาร์เลน บราวน์, คาร์ล เอ็ม. เพียร์ซีรายการ ค: บรรทัดฐานสำหรับกฎเกณฑ์ n-tuple ... // บทนำสู่การวิเคราะห์ - สปริงเกอร์, 2538. - หน้า 124. - ISBN 0387943692ดูหน้า 47-50 ด้วย
17. อัลเฟรด เกรย์, เอลซา อับบีนา, ไซมอน ซาลามอนเรขาคณิตเชิงอนุพันธ์สมัยใหม่ของเส้นโค้งและพื้นผิวด้วยคณิตศาสตร์ - ที่ 3 - CRC Press, 2549. - หน้า 194. - ISBN 1584884487
18. ราเชนทรา บาเทียการวิเคราะห์เมทริกซ์ - สปริงเกอร์, 1997. - หน้า 21. - ISBN 0387948465
19. สตีเฟน ดับเบิลยู. ฮอว์คิง อ้างถึงงาน. - 2548. - หน้า 4. - ISBN 0762419229
20. เอริก ดับเบิลยู. ไวส์สไตน์ CRC สารานุกรมคณิตศาสตร์ฉบับย่อ - ที่ 2 - 2003. - หน้า 2147. - ISBN 1584883472
21. อเล็กซานเดอร์ อาร์. พรัส

ตรวจสอบให้แน่ใจว่าสามเหลี่ยมที่คุณได้รับนั้นเป็นสามเหลี่ยมมุมฉาก เนื่องจากทฤษฎีบทพีทาโกรัสใช้ได้กับสามเหลี่ยมมุมฉากเท่านั้น ในรูปสามเหลี่ยมมุมฉาก มุมหนึ่งในสามมุมจะมีขนาด 90 องศาเสมอ

• มุมขวาในรูปสามเหลี่ยมมุมฉากจะแสดงด้วยไอคอนสี่เหลี่ยมจัตุรัส แทนที่จะเป็นเส้นโค้งที่แสดงถึงมุมเอียง

ติดป้ายด้านข้างของรูปสามเหลี่ยมตั้งชื่อขาว่า "a" และ "b" (ขาเป็นด้านที่ตัดกันเป็นมุมฉาก) และด้านตรงข้ามมุมฉากเป็น "c" (ด้านตรงข้ามมุมฉากเป็นด้านที่ใหญ่ที่สุดของสามเหลี่ยมมุมฉาก ซึ่งอยู่ตรงข้ามมุมขวา)

กำหนดว่าคุณต้องการหาด้านใดของสามเหลี่ยม.ทฤษฎีบทพีทาโกรัสช่วยให้คุณหาด้านใดๆ ของสามเหลี่ยมมุมฉากได้ (หากทราบอีกสองด้านที่เหลือ) พิจารณาว่าจะต้องค้นหาด้านใด (a, b, c)

• ตัวอย่างเช่น ให้ด้านตรงข้ามมุมฉากเท่ากับ 5 และให้ขาเท่ากับ 3 ในกรณีนี้ จำเป็นต้องหาขาที่สอง เราจะกลับมาที่ตัวอย่างนี้ในภายหลัง
• หากไม่ทราบอีกสองด้าน คุณจะต้องค้นหาความยาวของด้านที่ไม่ทราบด้านใดด้านหนึ่งจึงจะสามารถประยุกต์ใช้ทฤษฎีบทพีทาโกรัสได้ เมื่อต้องการทำเช่นนี้ ให้ใช้ฟังก์ชันตรีโกณมิติพื้นฐาน (หากคุณได้รับค่าของมุมเฉียงมุมใดมุมหนึ่ง)

แทนที่ค่าที่กำหนดให้กับคุณ (หรือค่าที่คุณพบ) ลงในสูตร a 2 + b 2 = c 2จำไว้ว่า a และ b เป็นขา และ c คือด้านตรงข้ามมุมฉาก

• ในตัวอย่างของเรา เขียน: 3² + b² = 5²

ยกกำลังสองแต่ละด้านที่รู้จักหรือทิ้งเลขยกกำลัง - คุณสามารถยกกำลังสองตัวเลขได้ในภายหลัง

• ในตัวอย่างของเรา เขียน: 9 + b² = 25

แยกด้านที่ไม่ทราบออกจากด้านหนึ่งของสมการเมื่อต้องการทำเช่นนี้ ให้โอนค่าที่ทราบไปยังอีกด้านหนึ่งของสมการ หากคุณพบด้านตรงข้ามมุมฉาก นั่นก็แสดงว่าในทฤษฎีบทพีทาโกรัสด้านตรงข้ามมุมฉากนั้นถูกแยกออกไปแล้วที่ด้านหนึ่งของสมการ (ดังนั้นคุณจึงไม่จำเป็นต้องทำอะไรเลย)

• ในตัวอย่างของเรา ให้ย้าย 9 ไปทางด้านขวาของสมการเพื่อแยกค่า b² ที่ไม่รู้จัก คุณจะได้b² = 16

หารากที่สองของทั้งสองข้างของสมการหลังจากที่คุณได้ค่าไม่ทราบค่า (กำลังสอง) อยู่ที่ด้านหนึ่งของสมการและมีค่าตัดแกน (ตัวเลข) อยู่ที่อีกด้านหนึ่ง

• ในตัวอย่างของเรา b² = 16 หารากที่สองของทั้งสองข้างของสมการแล้วได้ b = 4 ดังนั้น ขาที่สองคือ 4

ใช้ทฤษฎีบทพีทาโกรัสในชีวิตประจำวันของคุณเพราะสามารถนำไปใช้กับสถานการณ์ในทางปฏิบัติได้หลากหลาย เมื่อต้องการทำสิ่งนี้ ให้เรียนรู้ที่จะจดจำสามเหลี่ยมมุมฉากในชีวิตประจำวัน - ในสถานการณ์ใดๆ ที่วัตถุสองชิ้น (หรือเส้น) ตัดกันเป็นมุมฉาก และวัตถุชิ้นที่สาม (หรือเส้น) เชื่อมต่อ (ในแนวทแยง) ด้านบนของวัตถุสองชิ้นแรก (หรือ เส้นตรง) คุณสามารถใช้ทฤษฎีบทพีทาโกรัสเพื่อค้นหาด้านที่ไม่รู้จัก (หากทราบอีกสองด้านที่เหลือ)

• ตัวอย่าง: ให้บันไดพาดพิงอาคาร ฐานบันไดอยู่ห่างจากฐานผนัง 5 เมตร ด้านบนของบันไดสูงจากพื้นดิน 20 เมตร (ขึ้นไปที่ผนัง) บันไดยาวเท่าไรคะ?
  • “5 เมตรจากฐานกำแพง” หมายความว่า a = 5; “อยู่ห่างจากพื้นดิน 20 เมตร” หมายความว่า b = 20 (นั่นคือ คุณจะได้ขาสองข้างเป็นรูปสามเหลี่ยมมุมฉาก เนื่องจากผนังของอาคารและพื้นผิวโลกตัดกันเป็นมุมฉาก) ความยาวของบันไดคือความยาวของด้านตรงข้ามมุมฉากซึ่งไม่ทราบ
    • ก² + b² = ค²
    • (5)² + (20)² = ซี²
    • 25 + 400 = ซี²
    • 425 = ซี²
    • ค = √425
    • ค = 20.6 ดังนั้นความยาวของบันไดโดยประมาณคือ 20.6 เมตร

เกี่ยวกับทฤษฎีบทพีทาโกรัสและวิธีการพิสูจน์

จี. กลาสเซอร์,
นักวิชาการของ Russian Academy of Education, มอสโก

เกี่ยวกับทฤษฎีบทพีทาโกรัสและวิธีการพิสูจน์

บทความนี้ได้รับการตีพิมพ์โดยได้รับการสนับสนุนจากบริษัท Translation Master คุณต้องการการแปลคุณภาพสูงและรวดเร็วหรือไม่? ติดต่อหน่วยงานแปลที่มีการรับรองจาก Master of Translation ลูกค้าประจำของสำนักงานรับประกันคุณภาพการบริการ รวมถึงบริษัทรัสเซียที่มีชื่อเสียงหลายแห่ง เยี่ยมชมเว็บไซต์อย่างเป็นทางการของบริษัท www.masterperevoda.ru และเรียนรู้เพิ่มเติมเกี่ยวกับบริการที่พวกเขาให้

พื้นที่ของสี่เหลี่ยมจัตุรัสที่สร้างขึ้นบนด้านตรงข้ามมุมฉากของสามเหลี่ยมมุมฉากจะเท่ากับผลรวมของพื้นที่สี่เหลี่ยมจัตุรัสที่สร้างขึ้นบนขาของมัน...

นี่เป็นหนึ่งในทฤษฎีบทเรขาคณิตที่มีชื่อเสียงที่สุดในสมัยโบราณ เรียกว่าทฤษฎีบทพีทาโกรัส เกือบทุกคนที่เคยศึกษาการวัดระนาบรู้เรื่องนี้แม้กระทั่งตอนนี้ สำหรับฉันดูเหมือนว่าหากเราต้องการให้อารยธรรมต่างดาวทราบเกี่ยวกับการมีอยู่ของสิ่งมีชีวิตที่ชาญฉลาดบนโลก เราควรส่งรูปบุคคลพีทาโกรัสออกสู่อวกาศ ฉันคิดว่าหากสิ่งมีชีวิตที่มีความคิดสามารถยอมรับข้อมูลนี้ได้ ถ้าไม่มีการถอดรหัสสัญญาณที่ซับซ้อน พวกเขาจะเข้าใจว่าบนโลกมีอารยธรรมที่พัฒนาค่อนข้างมาก

นักปรัชญาชาวกรีกผู้มีชื่อเสียงและนักคณิตศาสตร์ Pythagoras แห่ง Samos ซึ่งเป็นผู้ตั้งชื่อทฤษฎีบทนั้นมีชีวิตอยู่เมื่อประมาณ 2.5 พันปีก่อน ข้อมูลชีวประวัติที่มาถึงเราเกี่ยวกับพีทาโกรัสนั้นไม่เป็นชิ้นเป็นอันและไม่น่าเชื่อถือ ตำนานมากมายเกี่ยวข้องกับชื่อของเขา เป็นที่ทราบกันดีอยู่แล้วว่าพีทาโกรัสเดินทางบ่อยครั้งในประเทศทางตะวันออกโดยไปเยือนอียิปต์และบาบิโลน ในอาณานิคมกรีกแห่งหนึ่งทางตอนใต้ของอิตาลี เขาได้ก่อตั้ง "โรงเรียนพีทาโกรัส" อันโด่งดัง ซึ่งมีบทบาทสำคัญในชีวิตทางวิทยาศาสตร์และการเมืองของกรีกโบราณ พีทาโกรัสเป็นผู้ให้เครดิตกับการพิสูจน์ทฤษฎีบทเรขาคณิตที่มีชื่อเสียง ตามตำนานที่นักคณิตศาสตร์ชื่อดังเผยแพร่ (Proclus, Plutarch ฯลฯ ) เชื่อกันมานานแล้วว่าทฤษฎีบทนี้ไม่เป็นที่รู้จักมาก่อนพีทาโกรัสดังนั้นชื่อ - ทฤษฎีบทพีทาโกรัส

อย่างไรก็ตาม ไม่ต้องสงสัยเลยว่าทฤษฎีบทนี้เป็นที่รู้จักก่อนปีทาโกรัสหลายปี ดังนั้น 1,500 ปีก่อนพีทาโกรัส ชาวอียิปต์โบราณรู้ว่าสามเหลี่ยมที่มีด้าน 3, 4 และ 5 เป็นมุมฉาก และใช้คุณสมบัตินี้ (นั่นคือ ทฤษฎีบทผกผันกับทฤษฎีบทพีทาโกรัส) เพื่อสร้างมุมขวาในการวางแผนที่ดินและ อาคารอาคาร แม้แต่ในปัจจุบันนี้ ผู้สร้างและช่างไม้ในชนบท เมื่อจะวางรากฐานของกระท่อมและประกอบชิ้นส่วนของกระท่อม ให้วาดรูปสามเหลี่ยมนี้เพื่อให้ได้มุมฉาก สิ่งเดียวกันนี้ทำเมื่อหลายพันปีก่อนในการสร้างพระวิหารอันงดงามในอียิปต์ บาบิโลน จีน และอาจจะในเม็กซิโก งานทางคณิตศาสตร์และดาราศาสตร์ของจีนที่เก่าแก่ที่สุดที่ตกทอดมาถึงเรา โจว ปี้ ซึ่งเขียนเมื่อประมาณ 600 ปีก่อนปีทาโกรัส ได้กล่าวถึงทฤษฎีบทพีทาโกรัส ท่ามกลางข้อเสนออื่นๆ ที่เกี่ยวข้องกับสามเหลี่ยมมุมฉาก ก่อนหน้านี้ชาวฮินดูรู้จักทฤษฎีบทนี้ด้วยซ้ำ ดังนั้น พีธากอรัสไม่ได้ค้นพบคุณสมบัติของสามเหลี่ยมมุมฉากนี้ เขาอาจเป็นคนแรกที่สรุปและพิสูจน์มัน ดังนั้นจึงย้ายจากสาขาปฏิบัติมาสู่สาขาวิทยาศาสตร์ เราไม่รู้ว่าเขาทำได้อย่างไร นักประวัติศาสตร์คณิตศาสตร์บางคนสันนิษฐานว่าการพิสูจน์ของพีทาโกรัสไม่ใช่พื้นฐาน แต่เป็นเพียงการยืนยัน ซึ่งเป็นการทดสอบคุณสมบัตินี้กับรูปสามเหลี่ยมบางประเภทโดยเฉพาะ โดยเริ่มจากสามเหลี่ยมมุมฉากหน้าจั่ว ซึ่งตามมาจากรูปที่ 1 อย่างเห็นได้ชัด 1.

ตั้งแต่สมัยโบราณ นักคณิตศาสตร์ได้ค้นพบการพิสูจน์ทฤษฎีบทพีทาโกรัสใหม่ๆ เพิ่มมากขึ้นเรื่อยๆ รวมถึงแนวคิดใหม่ๆ ในการพิสูจน์ทฤษฎีบทนี้มากขึ้นเรื่อยๆ เป็นที่ทราบกันดีว่ามีหลักฐานมากกว่าหนึ่งร้อยห้าสิบข้อ - เข้มงวดไม่มากก็น้อยมองเห็นได้ไม่มากก็น้อย แต่ความปรารถนาที่จะเพิ่มจำนวนยังคงอยู่ ฉันคิดว่า "การค้นพบ" การพิสูจน์ทฤษฎีบทพีทาโกรัสที่เป็นอิสระจะเป็นประโยชน์สำหรับเด็กนักเรียนยุคใหม่

เรามาดูตัวอย่างหลักฐานที่สามารถแนะนำทิศทางของการค้นหาดังกล่าวกัน

การพิสูจน์โดยใช้แนวคิดเรื่องขนาดเท่ากัน

ในกรณีนี้ เราสามารถพิจารณาหลักฐานได้ว่าสี่เหลี่ยมจัตุรัสที่สร้างขึ้นบนด้านตรงข้ามมุมฉากของสามเหลี่ยมมุมฉากที่กำหนดนั้น "ประกอบ" ขึ้นจากตัวเลขเดียวกันกับสี่เหลี่ยมจัตุรัสที่สร้างขึ้นด้านข้าง นอกจากนี้เรายังสามารถพิจารณาข้อพิสูจน์ที่ใช้การจัดเรียงผลรวมของตัวเลขใหม่และคำนึงถึงแนวคิดใหม่จำนวนหนึ่ง

• ในรูป 2 แสดงสี่เหลี่ยมจัตุรัส 2 ช่องที่เท่ากัน ความยาวของด้านของแต่ละสี่เหลี่ยมจัตุรัสคือ a + b แต่ละช่องสี่เหลี่ยมจะแบ่งออกเป็นส่วนต่างๆ ประกอบด้วยสี่เหลี่ยมจัตุรัสและสามเหลี่ยมมุมฉาก เป็นที่ชัดเจนว่าหากลบพื้นที่สี่เท่าของสามเหลี่ยมมุมฉากที่มีขา a, b ออกจากพื้นที่ของสี่เหลี่ยมจัตุรัส พื้นที่เท่ากันก็จะยังคงอยู่ เช่น c 2 = a 2 + b 2 . อย่างไรก็ตาม ชาวฮินดูโบราณซึ่งมีเหตุผลนี้มักจะไม่จดบันทึก แต่มาพร้อมกับภาพวาดด้วยคำเพียงคำเดียว: "ดูสิ!" ค่อนข้างเป็นไปได้ที่พีทาโกรัสเสนอข้อพิสูจน์แบบเดียวกัน

หลักฐานเพิ่มเติม

การพิสูจน์เหล่านี้ขึ้นอยู่กับการสลายตัวของสี่เหลี่ยมจัตุรัสที่สร้างขึ้นบนขาให้กลายเป็นรูป จากนั้นจึงนำสี่เหลี่ยมจัตุรัสที่สร้างบนด้านตรงข้ามมุมฉากมาบวกได้

โดยที่: ABC เป็นรูปสามเหลี่ยมมุมฉากที่มีมุมฉาก C; คเกี่ยวกับมินนิโซตา; ซีเค^มินนิโซตา; PO|มินนิโซตา; EF||มินนิโซตา

พิสูจน์ความเท่าเทียมกันของสามเหลี่ยมอย่างอิสระโดยการแบ่งช่องสี่เหลี่ยมที่สร้างบนขาและด้านตรงข้ามมุมฉาก

• ในรูป เลข 4 แสดงข้อพิสูจน์ทฤษฎีบทพีทาโกรัสโดยใช้ฉากกั้นของอัล-ไนริซิยาห์ ผู้วิจารณ์แบกแดดในยุคกลางเกี่ยวกับองค์ประกอบของยุคลิด ในส่วนนี้ สี่เหลี่ยมจัตุรัสที่สร้างขึ้นบนด้านตรงข้ามมุมฉากจะแบ่งออกเป็นสามเหลี่ยม 3 รูป และรูปสี่เหลี่ยม 2 รูป โดยที่: ABC เป็นรูปสามเหลี่ยมมุมฉากที่มีมุมฉาก C; DE = BF

พิสูจน์ทฤษฎีบทโดยใช้ส่วนนี้

• จากการพิสูจน์ของอัล-ไนริซิยา พบว่ามีการสลายตัวของสี่เหลี่ยมจัตุรัสให้กลายเป็นตัวเลขที่เท่ากันเป็นคู่ (รูปที่ 5 ที่นี่ ABC เป็นรูปสามเหลี่ยมมุมฉากที่มีมุมฉาก C)

• ข้อพิสูจน์อีกประการหนึ่งโดยวิธีสลายสี่เหลี่ยมจัตุรัสให้เป็นส่วนเท่าๆ กัน เรียกว่า “ล้อที่มีใบมีด” แสดงไว้ในรูปที่ 1 6. ตรงนี้: ABC เป็นรูปสามเหลี่ยมมุมฉากที่มีมุมฉาก C; O คือจุดศูนย์กลางของจัตุรัสที่สร้างด้านใหญ่ เส้นประที่ผ่านจุด O นั้นตั้งฉากหรือขนานกับด้านตรงข้ามมุมฉาก

• การสลายตัวของกำลังสองนี้น่าสนใจเพราะว่ารูปสี่เหลี่ยมขนมเปียกปูนที่มีขนาดเท่าๆ กันเป็นคู่สามารถจับคู่กันได้โดยการแปลแบบขนาน การพิสูจน์ทฤษฎีบทพีทาโกรัสอื่นๆ อีกมากมายสามารถเสนอได้โดยใช้การสลายตัวของกำลังสองให้เป็นตัวเลข

หลักฐานโดยวิธีการทำให้เสร็จ

สาระสำคัญของวิธีนี้คือการเพิ่มตัวเลขที่เท่ากันลงในสี่เหลี่ยมที่สร้างขึ้นบนขาและสี่เหลี่ยมที่สร้างขึ้นบนด้านตรงข้ามมุมฉากในลักษณะที่ได้ตัวเลขที่เท่ากัน

ความถูกต้องของทฤษฎีบทพีทาโกรัสตามมาจากขนาดเท่ากันของ AEDFPB และ ACBNMQ รูปหกเหลี่ยม นี่ซี.เกี่ยวกับ EP, เส้น EP แบ่ง AEDFPB หกเหลี่ยมออกเป็นสองจตุรัสเท่าๆ กัน, เส้น CM แบ่ง ACBNMQ หกเหลี่ยมออกเป็นสองจตุรัสที่เท่ากัน; การหมุนเครื่องบิน 90° รอบจุดศูนย์กลาง A จะจับคู่ AEPB รูปสี่เหลี่ยมเข้ากับ ACMQ รูปสี่เหลี่ยม

ตอนนี้ให้เราพิสูจน์ว่าตัวเลขที่ถูกลบในกรณีแรกมีขนาดเท่ากับตัวเลขที่ถูกลบในกรณีที่สอง

KLOA = ACPF = ACED = a 2 ;

LBO = CBMP = CBNQ = b 2 ;

AKGB = AKLO + LBO = c 2 ;

ดังนั้น c 2 = a 2 + b 2

OCLP = ACLF = ACED = ข 2 ;

CBML = CBNQ = a 2 ;

OBMP = ABMF = ค 2 ;

OBMP = OCLP + CBML;

จากที่นี่

ค 2 = ก 2 + ข 2 .

• ข้าว. รูปที่ 11 แสดงให้เห็นหลักฐานต้นฉบับอีกประการหนึ่งที่เสนอโดยฮอฟฟ์มันน์
  ที่นี่: สามเหลี่ยม ABC ที่มีมุมขวา C; ส่วน BF ตั้งฉากกับ CB และเท่ากับส่วน BE ตั้งฉากกับ AB และเท่ากับส่วน AD ตั้งฉากกับ AC และเท่ากับมัน คะแนน F, C, D อยู่ในบรรทัดเดียวกัน รูปสี่เหลี่ยม ADFB และ ACBE มีขนาดเท่ากัน เนื่องจาก ABF=ECB; สามเหลี่ยม ADF และ ACE มีขนาดเท่ากัน ลบออกจากรูปสี่เหลี่ยมขนมเปียกปูนทั้งสองรูปสามเหลี่ยม ABC ที่พวกมันแบ่งกัน เราก็จะได้

วิธีการพิสูจน์พีชคณิต

ในรูป 13 ABC – สี่เหลี่ยม, C – มุมขวา, CM^ AB, b 1 – เส้นโครงของขา b ลงบนด้านตรงข้ามมุมฉาก, a 1 – เส้นโครงของขา a บนด้านตรงข้ามมุมฉาก, h – ความสูงของสามเหลี่ยมที่ลากไปยังด้านตรงข้ามมุมฉาก

จากข้อเท็จจริงที่ว่า D ABC มีความคล้ายคลึงกับ D ACM จึงเป็นไปตามนี้

ข 2 = CB 1 ; (1)

จากข้อเท็จจริงที่ว่า D ABC มีความคล้ายคลึงกับ D BCM ดังต่อไปนี้

ก 2 = แคลิฟอร์เนีย 1 . (2)

เมื่อบวกความเท่าเทียมกัน (1) และ (2) ทีละเทอม เราจะได้ a 2 + b 2 = cb 1 + ca 1 = c(b 1 + a 1) = c 2

หากพีทาโกรัสเสนอข้อพิสูจน์เช่นนั้น เขาก็คุ้นเคยกับทฤษฎีบทเรขาคณิตที่สำคัญหลายข้อที่นักประวัติศาสตร์คณิตศาสตร์สมัยใหม่มักเชื่อว่าเป็นของยุคลิด

ด้วยเหตุนี้ c 2 =a 2 +b 2

ในวินาที

เมื่อเทียบนิพจน์เหล่านี้เข้าด้วยกัน เราจะได้ทฤษฎีบทพีทาโกรัส

• มีการพิสูจน์ทฤษฎีบทพีทาโกรัสมากมาย ซึ่งดำเนินการโดยแต่ละวิธีที่อธิบายไว้ หรือใช้วิธีต่างๆ รวมกัน เมื่อสรุปการทบทวนตัวอย่างการพิสูจน์ต่างๆ เรานำเสนอภาพวาดเพิ่มเติมที่แสดงให้เห็นแปดวิธีที่ถูกอ้างอิงในองค์ประกอบของยุคลิด (รูปที่ 16 - 23) ในภาพวาดเหล่านี้ รูปพีทาโกรัสแสดงด้วยเส้นทึบ และโครงสร้างเพิ่มเติมจะแสดงด้วยเส้นประ

1. ฟาน เดอร์ วาร์เดน บี.แอล. วิทยาศาสตร์ตื่นตัว. คณิตศาสตร์ของอียิปต์โบราณ บาบิโลน และกรีซ ม., 1959.
2. เกลเซอร์ จี.ไอ. ประวัติคณิตศาสตร์ที่โรงเรียน ม., 1982.
3. Yelensky Shch ตามรอยพีทาโกรัส ม., 1961.
4. ทฤษฎีบทของลิทซ์แมน วี. พีทาโกรัส ม., 1960.
5. สโกเพ็ตส์ Z.A. เพชรประดับทางเรขาคณิต ม., 1990.

ทฤษฎีบทพีทาโกรัส

ชะตากรรมของทฤษฎีบทและปัญหาอื่น ๆ นั้นแปลกประหลาด... ตัวอย่างเช่นจะอธิบายได้อย่างไรว่าความสนใจเป็นพิเศษในส่วนของนักคณิตศาสตร์และผู้ชื่นชอบคณิตศาสตร์ต่อทฤษฎีบทพีทาโกรัส? เหตุใดพวกเขาหลายคนจึงไม่พอใจกับหลักฐานที่ทราบอยู่แล้ว แต่พบหลักฐานของตนเอง ทำให้จำนวนหลักฐานเพิ่มขึ้นหลายร้อยตลอดยี่สิบห้าศตวรรษที่ค่อนข้างคาดเดาได้
เมื่อพูดถึงทฤษฎีบทพีทาโกรัส สิ่งผิดปกติจะเริ่มต้นด้วยชื่อของมัน เชื่อกันว่าไม่ใช่พีทาโกรัสที่เป็นคนคิดค้นสิ่งนี้ขึ้นเป็นครั้งแรก ถือว่ายังเป็นที่น่าสงสัยว่าเขาให้หลักฐานมาด้วย หากพีธากอรัสเป็นคนจริง (บางคนถึงกับสงสัยเรื่องนี้!) เขาน่าจะมีชีวิตอยู่ในศตวรรษที่ 6-5 พ.ศ จ. ตัวเขาเองไม่ได้เขียนอะไรเลยเรียกตัวเองว่าเป็นนักปรัชญาซึ่งในความเข้าใจของเขาหมายถึง "มุ่งมั่นเพื่อปัญญา" และก่อตั้งสหภาพพีทาโกรัสซึ่งสมาชิกศึกษาดนตรี ยิมนาสติก คณิตศาสตร์ ฟิสิกส์ และดาราศาสตร์ เห็นได้ชัดว่าเขายังเป็นนักพูดที่ยอดเยี่ยมด้วยตามหลักฐานตามตำนานต่อไปนี้เกี่ยวกับการที่เขาอยู่ในเมือง Croton: “ การปรากฏตัวครั้งแรกของ Pythagoras ต่อหน้าผู้คนใน Croton เริ่มต้นด้วยคำพูดต่อชายหนุ่มซึ่งเขาเป็นเช่นนั้น เข้มงวด แต่ในขณะเดียวกันก็สรุปหน้าที่ของชายหนุ่มได้อย่างน่าทึ่งและผู้เฒ่าในเมืองก็ขออย่าทิ้งพวกเขาไปโดยไม่ได้รับคำแนะนำ ในสุนทรพจน์ครั้งที่สองนี้ พระองค์ทรงชี้ให้เห็นถึงความถูกต้องตามกฎหมายและความบริสุทธิ์ของศีลธรรมเป็นรากฐานของครอบครัว ในอีกสองช่วงถัดมาพระองค์ทรงปราศรัยกับเด็กและสตรี ผลที่ตามมาจากสุนทรพจน์ครั้งสุดท้ายซึ่งเขาประณามความฟุ่มเฟือยเป็นพิเศษก็คือชุดล้ำค่าหลายพันชุดถูกส่งไปยังวิหารแห่งเฮรา เพราะไม่มีผู้หญิงสักคนเดียวกล้าปรากฏตัวบนถนนอีกต่อไป...” อย่างไรก็ตาม แม้แต่ใน คริสต์ศตวรรษที่ 2 นั่นคือ 700 ปีต่อมา ผู้คนจริงๆ อาศัยและทำงาน เป็นนักวิทยาศาสตร์ที่ไม่ธรรมดาซึ่งเห็นได้ชัดว่าอยู่ภายใต้อิทธิพลของสหภาพพีทาโกรัส และผู้ที่มีความเคารพอย่างมากต่อสิ่งที่ตามตำนาน พีทาโกรัสสร้างขึ้น
ไม่ต้องสงสัยเลยว่าความสนใจในทฤษฎีบทนี้เกิดจากข้อเท็จจริงที่ว่าทฤษฎีบทนี้ครองตำแหน่งศูนย์กลางด้านคณิตศาสตร์แห่งหนึ่ง และจากความพึงพอใจของผู้เขียนบทพิสูจน์ที่เอาชนะความยากลำบากที่กวีชาวโรมัน Quintus Horace Flaccus ซึ่งอยู่ก่อนยุคของเราก็พูดดีว่า: “เป็นการยากที่จะแสดงข้อเท็จจริงที่รู้จักกันดี” .
ในตอนแรก ทฤษฎีบทได้สร้างความสัมพันธ์ระหว่างพื้นที่สี่เหลี่ยมจัตุรัสที่สร้างบนด้านตรงข้ามมุมฉากกับขาของสามเหลี่ยมมุมฉาก:
.
สูตรพีชคณิต:
ในสามเหลี่ยมมุมฉาก กำลังสองของความยาวของด้านตรงข้ามมุมฉากจะเท่ากับผลรวมของกำลังสองของความยาวของขา
นั่นคือ แทนความยาวของด้านตรงข้ามมุมฉากของสามเหลี่ยมด้วย c และความยาวของขาด้วย a และ b: a 2 + b 2 =c 2 สูตรของทฤษฎีบททั้งสองสูตรมีค่าเท่ากัน แต่สูตรที่สองนั้นเป็นสูตรพื้นฐานมากกว่า ไม่ต้องการแนวคิดเรื่องพื้นที่ กล่าวคือ ข้อความที่สองสามารถตรวจสอบได้โดยไม่ต้องรู้อะไรเลยเกี่ยวกับพื้นที่ และโดยการวัดเฉพาะความยาวของด้านของสามเหลี่ยมมุมฉากเท่านั้น
ทฤษฎีบทคอนเวิร์สพีทาโกรัส สำหรับจำนวนบวกสามเท่าใดๆ a, b และ c แบบนั้น
a 2 + b 2 = c 2 มีสามเหลี่ยมมุมฉากที่มีขา a และ b และด้านตรงข้ามมุมฉาก c

การพิสูจน์

ปัจจุบันมีการบันทึกไว้ 367 ข้อพิสูจน์ของทฤษฎีบทนี้ในวรรณกรรมทางวิทยาศาสตร์ อาจเป็นไปได้ว่าทฤษฎีบทพีทาโกรัสอาจเป็นทฤษฎีบทเดียวที่มีการพิสูจน์จำนวนที่น่าประทับใจเช่นนี้ ความหลากหลายดังกล่าวสามารถอธิบายได้ด้วยความสำคัญพื้นฐานของทฤษฎีบทสำหรับเรขาคณิตเท่านั้น
แน่นอนว่าตามแนวคิดแล้วทั้งหมดสามารถแบ่งออกเป็นคลาสจำนวนเล็กน้อยได้ สิ่งที่มีชื่อเสียงที่สุด: การพิสูจน์โดยวิธีพื้นที่, การพิสูจน์ตามสัจพจน์และแปลกใหม่ (เช่น การใช้สมการเชิงอนุพันธ์)

ผ่านรูปสามเหลี่ยมที่คล้ายกัน

การพิสูจน์สูตรพีชคณิตต่อไปนี้เป็นการพิสูจน์ที่ง่ายที่สุด ซึ่งสร้างขึ้นจากสัจพจน์โดยตรง โดยเฉพาะอย่างยิ่งไม่ใช้แนวคิดเรื่องพื้นที่ของรูป
ให้ ABC เป็นสามเหลี่ยมมุมฉากที่มีมุมฉาก C วาดระดับความสูงจาก C และแทนฐานด้วย H สามเหลี่ยม ACH คล้ายกับสามเหลี่ยม ABC ที่มุมสองมุม
ในทำนองเดียวกัน สามเหลี่ยม CBH ก็คล้ายกับ ABC โดยการแนะนำสัญกรณ์

เราได้รับ

สิ่งที่เทียบเท่า

เมื่อบวกกันแล้วเราก็จะได้

หรือ

การพิสูจน์โดยใช้วิธีพื้นที่

ข้อพิสูจน์ด้านล่าง แม้จะดูเรียบง่าย แต่ก็ไม่ง่ายเลย พวกมันทั้งหมดใช้คุณสมบัติของพื้นที่ ซึ่งการพิสูจน์นั้นซับซ้อนกว่าการพิสูจน์ทฤษฎีบทพีทาโกรัสเสียอีก

พิสูจน์ผ่านการเสริมสมมูล

1. วางสามเหลี่ยมมุมฉากสี่อันเท่ากันดังแสดงในรูป
2. รูปสี่เหลี่ยมขนมเปียกปูนที่มีด้าน c คือรูปสี่เหลี่ยมจัตุรัส เนื่องจากผลรวมของมุมแหลมสองมุมคือ 90° และมุมตรงคือ 180°
3. ด้านหนึ่งมีพื้นที่ของรูปทั้งหมดเท่ากันกับพื้นที่ของสี่เหลี่ยมจัตุรัสที่มีด้าน (a + b) และอีกด้านหนึ่งเท่ากับผลรวมของพื้นที่ของสามเหลี่ยมสี่รูปและ จัตุรัสด้านใน



Q.E.D.

การพิสูจน์ด้วยความเท่าเทียมกัน

ตัวอย่างของข้อพิสูจน์ประการหนึ่งแสดงไว้ในภาพวาดด้านขวา โดยที่สี่เหลี่ยมจัตุรัสที่สร้างบนด้านตรงข้ามมุมฉากจะถูกจัดเรียงใหม่เป็นสี่เหลี่ยมจัตุรัสสองอันที่สร้างอยู่บนขา

ข้อพิสูจน์ของยุคลิด

แนวคิดในการพิสูจน์ของ Euclid มีดังนี้ ลองพิสูจน์ว่าพื้นที่ครึ่งหนึ่งของสี่เหลี่ยมจัตุรัสที่สร้างขึ้นบนด้านตรงข้ามมุมฉากเท่ากับผลรวมของพื้นที่ครึ่งหนึ่งของสี่เหลี่ยมจัตุรัสที่สร้างบนขา และจากนั้นพื้นที่ของ สี่เหลี่ยมใหญ่และสี่เหลี่ยมเล็กสองอันมีค่าเท่ากัน ลองดูภาพวาดทางด้านซ้าย บนนั้นเราสร้างสี่เหลี่ยมที่ด้านข้างของสามเหลี่ยมมุมฉากและดึงรังสี s จากจุดยอดของมุมฉาก C ซึ่งตั้งฉากกับด้านตรงข้ามมุมฉาก AB มันตัดสี่เหลี่ยม ABIK ที่สร้างขึ้นบนด้านตรงข้ามมุมฉากออกเป็นสี่เหลี่ยมสองอัน - BHJI และ HAKJ ตามลำดับ ปรากฎว่าพื้นที่ของสี่เหลี่ยมเหล่านี้เท่ากับพื้นที่สี่เหลี่ยมที่สร้างขึ้นบนขาที่สอดคล้องกันทุกประการ ลองพิสูจน์ว่าพื้นที่ของสี่เหลี่ยม DECA เท่ากับพื้นที่ของสี่เหลี่ยม AHJK ในการทำเช่นนี้เราจะใช้การสังเกตเสริม: พื้นที่ของสามเหลี่ยมที่มีความสูงและฐานเท่ากับ สี่เหลี่ยมที่กำหนดมีค่าเท่ากับครึ่งหนึ่งของพื้นที่สี่เหลี่ยมที่กำหนด นี่เป็นผลมาจากการกำหนดพื้นที่ของสามเหลี่ยมเป็นครึ่งหนึ่งของผลคูณของฐานและความสูง จากการสังเกตนี้เป็นไปตามว่าพื้นที่ของสามเหลี่ยม ACK เท่ากับพื้นที่ของสามเหลี่ยม AHK (ไม่แสดงในรูป) ซึ่งจะเท่ากับครึ่งหนึ่งของพื้นที่สี่เหลี่ยม AHJK ตอนนี้ให้เราพิสูจน์ว่าพื้นที่ของสามเหลี่ยม ACK เท่ากับครึ่งหนึ่งของพื้นที่ DECA สี่เหลี่ยมจัตุรัสด้วย สิ่งเดียวที่ต้องทำเพื่อสิ่งนี้คือการพิสูจน์ความเท่าเทียมกันของสามเหลี่ยม ACK และ BDA (เนื่องจากพื้นที่ของสามเหลี่ยม BDA เท่ากับครึ่งหนึ่งของพื้นที่ของสี่เหลี่ยมตามคุณสมบัติข้างต้น) ความเท่าเทียมกันนี้ชัดเจน สามเหลี่ยมเท่ากันทั้งสองข้างและมีมุมระหว่างสามเหลี่ยมเหล่านั้น กล่าวคือ - AB=AK,AD=AC - ความเท่าเทียมกันของมุม CAK และ BAD นั้นพิสูจน์ได้ง่ายโดยวิธีการเคลื่อนที่: เราหมุนสามเหลี่ยม CAK 90° ทวนเข็มนาฬิกา จากนั้นจะเห็นได้ชัดว่าด้านที่สอดคล้องกันของสามเหลี่ยมทั้งสองใน คำถามจะตรงกัน (เนื่องจากมุมที่จุดยอดของรูปสี่เหลี่ยมจัตุรัสคือ 90°) เหตุผลสำหรับความเท่าเทียมกันของพื้นที่ของสี่เหลี่ยมจัตุรัส BCFG และสี่เหลี่ยม BHJI นั้นคล้ายกันโดยสิ้นเชิง ดังนั้นเราจึงพิสูจน์ว่าพื้นที่ของสี่เหลี่ยมจัตุรัสที่สร้างขึ้นบนด้านตรงข้ามมุมฉากนั้นประกอบด้วยพื้นที่สี่เหลี่ยมจัตุรัสที่สร้างขึ้นบนขา

หลักฐานของเลโอนาร์โด ดา วินชี

องค์ประกอบหลักของการพิสูจน์คือความสมมาตรและการเคลื่อนที่

ลองพิจารณาภาพวาดดังที่เห็นได้จากความสมมาตร ส่วน CI จะตัดสี่เหลี่ยมจัตุรัส ABHJ ออกเป็นสองส่วนที่เหมือนกัน (เนื่องจากสามเหลี่ยม ABC และ JHI เท่ากันในการก่อสร้าง) เมื่อใช้การหมุนทวนเข็มนาฬิกา 90 องศา เราจะเห็นความเท่าเทียมกันของตัวเลขที่แรเงา CAJI และ GDAB ตอนนี้เห็นได้ชัดว่าพื้นที่ของร่างที่เราแรเงานั้นเท่ากับผลรวมของครึ่งหนึ่งของพื้นที่สี่เหลี่ยมที่สร้างบนขาและพื้นที่ของสามเหลี่ยมดั้งเดิม ในทางกลับกัน จะเท่ากับครึ่งหนึ่งของพื้นที่สี่เหลี่ยมจัตุรัสที่สร้างขึ้นบนด้านตรงข้ามมุมฉาก บวกกับพื้นที่ของสามเหลี่ยมเดิม ขั้นตอนสุดท้ายในการพิสูจน์เป็นหน้าที่ของผู้อ่าน